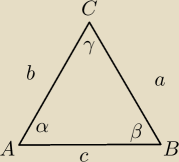
Dany jest trójką ostrokątny ABC o bokach długości a,b,c i kątach α,β,γ (zobacz r kamczatka: Dany jest trójką ostrokątny ABC o bokach długości a,b,c i kątach α,β,γ (zobacz rysunek). Wykaż że

a2+b2−c2
	= tgα * ctgγ
b2+c2−a2

kamczatka: ?

Bogdan:

	a		sinα
Z tw. sinusów:		=
	c		sonγ

Z tw. cosinusów: a² + b² − c² = 2ab cosγ, b² + c² − a² = 2bc cosα

a2 + b2 − c2		2ab cosγ		a		cosγ
	=		=		*		=
b2 + c2 − a2		2bc cosα		c		cosα

	sinα		cosγ
=		*		= tgα * ctgγ
	sonγ		cosα

Hajtowy: Panie Bogdanie, twierdzenie sinusów, cosinusów nie ma szans by pojawiło się na maturze podstawowej, ale można tym sposobem rozwiązywać zadania, prawda? kamczatka R zdajesz z matmy?

Bogdan: Prawda

Bogdan: Kiedyś twierdzenie sinusów i cosinusów było w programie nauczania zasadniczych szkół zawodowych

kamczatka: zdaje, od amatora do rozszerzenia

kamczatka:

	a
czemu w 3 linijce potem jest		?
	c

drzewo: ?

kamczatka: dobra już wiem

kamczatka: Jeszcze nie rozumiem jednak ostatniej linijki czemu

sinα		cosγ
	*		= tgα*ctgγ?
sinγ		cosα