Wykazanie z definicji Nieuchwytny: Jak wykazać z definicji że funkcja jest malejąca lub rosnąca w danym zbiorze.

zawodus: (rosnąca) wziąć dwa punkty ze zbioru i pokazać, że x₁<x₂ ⇒f(x₁)<f(x₂)

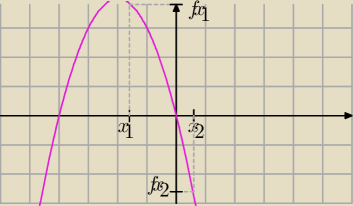
Nieuchwytny: Dla przykładu f(x)=−x²−4x jest malejąca w zbiorze (−2,+∞) x₁>x₂ ⇒f(x₁)>f(x₂) x₁=−3 x₂=−4 f(x₁)=−9+12=3 f(x₂)=0 3>0 Tak mamy to zapisywać?

WueR: Jesli jest malejaca na (−2,∞), to: dla dowolnych x₁,x₂∊(−2,∞): x₁<x₂⇒f(x₁)>f(x₂). Najpierw postaraj sie zrozumiec te definicje. Ponadto, pokazujemy wtedy, ze dla wszystkich argumentow z tego przedzialu tak jest, nie dla wybranych (bo inaczej pokazujemy, ze tak jest tylko dla tych wybranych).

Nieuchwytny: Można to zapisać w poniższy sposób: x₁<x₂ f(x₁)−f(x₂)<0 f(x₁)−f(x₂)=−(x₁)²−4x+(x₂)²+4x₂ f(x₁)−f(x₂)=(x₂−x₁)(x₁+x₂+4) f(x₁)<f(x₂)

Nieuchwytny: ?

WueR: Zatem pokazmy, ze f(x)=−x²−4x jest malejaca na (−2,∞). Ustalmy dowolne x₁,x₂ z przedzialu (−2,∞) ale takie, ze x₁<x₂ Teza: f(x₁)>f(x₂) [rownowaznie po odjeciu f(x₂) stronami mamy: f(x₁)−f(x₂)>0] Wtedy f(x₁) = −x₁²−4x₁, f(x₂)=−x₂²−4x₂ i mamy: f(x₁)−f(x₂) = −x₁²−4x₁ − [−x₂²−4x₂] = −x₁²−4x₁+x₂²+4x₂ = x₂²−x₁²+4x₂−4x₁ = =(x₂−x₁)(x₂+x₁)+4(x₂−x₁) = (x₂−x₁)(x₂+x₁+4) Zauwazmy, ze jesli x₁<x₂, to naturalnie x₂−x₁>0, oraz jesli oba argumenty sa z wczesniej wspomnianego przedzialu, to rowniez x₂+x₁+4>0, zatem powyzszy iloczyn jest wiekszy od zera. Z dowolnosci wyboru wnioskujemy, ze jest tak dla dowolnych x₁,x₂ z rozwazanego przedzialu, tzn. (−2,∞)

WueR: Mozna tak zapisac, ale potrzebne sa komentarze. Jak wstawisz ciag znaczkow to niekoniecznie ktos bedzie wiedzial, o co Ci chodzi. No i na sprawdzianach czy kolokwiach konieczne sa oczywiscie przeksztalcenia.

Nieuchwytny: Dziękuję bardzo za wytłumaczenie.

WueR: Aha, a ja dalej nie zauwazylem bledu w poscie z godziny 11:18. Jezeli pokazujemy, ze funkcja jest malejaca, to ma byc: x₁<x₂⇒f(x₁)>f(x₂) Tzn wartosc dla argumentu mniejszego (tutaj x₁) jest wieksza od tej dla argumentu wiekszego (x₂) .