pochodna Uri: Witam Mamy takie przykłady:

	⎧	2x + 8 dla x∊(−∞, −1)
a) f(x) =	⎨		; x0 = −1;
	⎩	x2 − 4x dla x∊<−1, +∞)

	⎧	x − 3 dla x∊(−∞, 3>
b) f(x) =	⎨		; x0 = 3;
	⎩	−x + 3 dla x∊(3, +∞)

W pierwszym przypadku funkcja nie jest ciągła wobec tego nie jest różniczkowalna w punkcie x₀. W drugim przypadku Funkcja jest ciągła i nie jest różniczkowalna w punkcie x₀ bo pochodne jednostronne są różne. Moje pytanie: Czy trzeba sprawdzać warunek ciągłości funkcji? Wydaje mi się, że jeżeli policzę pochodne jednostronne i będą równe to funkcja będzie różniczkowalna w pewnym punkcie x₀.

WueR: Jezeli pochodne jednostronne w punkcie x sa rowne, to funkcja jest rozniczkowalna w x. Jezeli funkcja jest rozniczkowalna w x, to jest w tym punkcie ciagla.

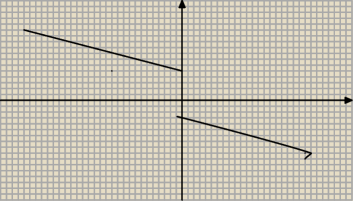
PW: Pochodne lewo− i prawostronna są równe, a kurde, funkcja jest nieciągła! (proszę wybaczyć niedokładność rysunku, chyba wiadomo o co idzie).

PW: Post Scriptum. Ten rysunek to prowokacja spowodowana pytaniem Uri "czy trzeba sprawdzać ciągłość" (wyczuwam, że nie do końca rozumie pojęcie pochodnej jednostronnej). Ciekawe, czy ktoś wyjaśni, co w rysunku i komentarzu z 15:39 jest "nie tak".

pomocnik: A dlaczego pochodne lewo− i prawostronna są równe?

PW: Kontynuując prowokację odpowiem − to jasne, przecież pochodna to tangens kąta nachylenia stycznej do wykresu (starałem się narysować dwie proste nachylone pod tym samym kątem).

pomocnik: Więc podłapuję, pochodna (w punkcie) to tg, ale czy pochodna jednostronna też?

PW: Też, tyle że skradamy się punktami w dziedzinie z jednej strony punktu x₀ (w definicji pochodnej w punkcie x₀ takiego ograniczenia nie ma). Klasyczny przykład to f(x) = |x| − pochodne lewo− i prawostronna w x₀ = 0 istnieją, ale są różne, lewostronna jest równa −1, a prawostronna jest równa 1. Co jest "oszukane" w rysunku i komentarzu z 15:39?

pomocnik: W rysunku problem polega na tym, że nie wiadomo, jaka jest wartość funkcji w 0. A z tymi tg i pochodnymi jednostronnymi, to chyba trochę naciągane.

Uri: Odnośnie rysunku PW pochodne są jednostronne, czyli są również ciągłe jednostronnie, ale trzeba jeszcze policzyć wartość dla argumentu x_o i sprawdzić czy jest równa z granicami ciągłości. O to chodziło?

pomocnik: W tym sęk, że co najmniej jedna z pochodnych jednostronnych nie będzie istnieć.

PW: Tak, pomocnik ma rację. Nie zaznaczyłem "kółka pełnego" i "kółka pustego", więc nie wiadomo, czy lewo−, czy prawostronna w zerze nie będzie istnieć, ale jedna z nich nie istnieje. Załóżmy, że f(5) = ax+5 dla x≤0 oraz f(x) = ax−3 dla x>0 oraz h>0. Iloraz różnicowy dla pochodnej lewostronnej w zerze ma postać

	a•(0−h)+5 − (a•0+5)		−ah
		=		= a,
	−h		−h

tak więc pochodna lewostronna w zerze jest równa a. Iloraz różnicowy dla pochodnej prawostronnej w zerze ma postać

	a(0+h)−3 − (a•0+5)		ah−8		8
		=		= a −		,
	h		h		h

a takie coś przy h→0 nie ma skończonej granicy. Przykład pouczający, ale Uri powinien wnioskować poczynając od twierdzenia − Jeżeli funkcja ma pochodną w punkcie x₀, to jest w tym punkcie ciągła, czyli to samo przez kontrapozycję: − Jeżeli funkcja nie jest ciągła w punkcie x₀, to nie ma w tym punkcie pochodnej. Natomiast gdy jest ciągła i pochodne jednostronne (istnieją i) są równe, to oczywiście pochodna istnieje.

pomocnik: Modyfikując przykład PW f(x) = ax+5 dla x<0, f(x) = ax−3 dla x>0 i f(0)=0 mamy przykład na to, że obie pochodne jednostronne nie istnieją (oczywiście w 0).