PROŚBA Matejko: Mogę prosić o zbiór zadań z trygonometrii, ale tylko z wyznaczania zbioru wartości jakiejś funkcji bo chciałbym się tego nauczyć bo jeszcze nie umiem.

Matejko: ?

5-latek: Czesc . Tez tego szukalem zeby bylo z rozwiazaniami . Niestety nie znalazlem . takze musisz szukac w wyszkiwarce lub na innych forach .

zawodus: 5−latek czas napisać własną książkę

5-latek: Chcialbym Ale ja jestem tylko biednym Technikiem Mechanizacji Rolnictwa

52: a)y= −sin²x+4sinx+12 b)y=cos²2x−cos2x−2 Odp. a)<7,15>

	1
b)<−2		,0)
	4

Matejko: o 52. super moge prosić o więcej przykładów?

52: c) y=tg³x−tg²x+tgx−1

	1
d) y=
	cos2x−2cosx−8

Odp. c)R

	1		1
d)<−		,−		>
	5		9

Domel: Witam wszystkich 5−latek a jakież to województwo kształciło technika mech−rol − jeszcze się okaże, że my po jednej szkole

Matejko: jak zrobić a) np?

5-latek: Czesc Domel Grodków woj. oplskie

Matejko: mogę o wyjaśnienie a) poprosić?

52: Niech sin x = t gdzie t∊<−1,1> t=−t²+4t+12

	b		4		4
tw=−		=−		=		=2 ∉<−1,1>
	2a		2*(−1)		2

Wierzchołek funkcji nie należy do wcześniej ustalonego warunku. Szukamy największej i najmniejszej wartości funkcji dla t∊<−1,1> Wiemy że największa i najmniejsza wartość funkcji znajduje się na końcach naszego warunku t∊<−1,1> f(1)=−1+4+12=15 f(−1)=−1−4+12=7 ZWf : y∊<7,15>

Domel: No a tu − Gronowo − kuj−pom

5-latek: WItam To prawie cala Polska wszserz A ktory rocznik bo ja 1973−1978

Domel: A mój − szlachetny 82 − 87

Matejko: a jak rozwiązać b)?

Matejko: tak samo d dlaczego wierzchołek nie jest najmniejszą wartością nie rozumiem

Domel: b)y=cos²2x−cos2x−2 I fikołek cos2x = t ∧ t∊<−1; 1> t² − t − 2 = 0 ekstremum (u nas minimum) funkcji:

	−b		1
tW =		=		−> ymin = tW2 − tW − 2
	2a		2

	1		1		1
ymin =		−		− 2 = −2
	4		2		4

a maximum dla t∊<−1; 1> y(−1) = 1 + 1 − 2 = 0 y(1) = 1 − 1 − 2 = −2 y₁ jest max w przedziale <−1; 1> więc

	1
y∊<−2		; 0>
	4

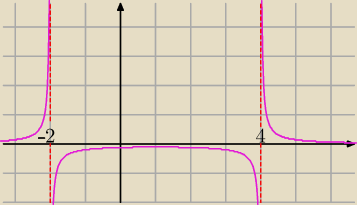
Domel: Jeszcze odnośnie zad. b − t_W mieści się w dziedzinie <−1; 1> dlatego mamy punkt minimum

	1
d) y=
	cos2x−2cosx−8

i znowu: cosx = t ∧ t∊<−1; 1>

	1
y =		−. mianownik musi być ≠ 0
	t2 − 2t − 8

t² − 2t − 8 = 0 => Δ = 4 + 32 = 36 => √Δ = 6

	2−6
t1 =		= −2
	2

	2+6
t2 =		= 4
	2

Oba pierwiastki nie należą do przedziału <−1; 1> dlatego w tym przedziale mianownik nie będzie równy 0 − oba pierwiastki są jednocześnie asymptotami dla których y→±oo Ekstremum (min) funkcji y₂ = t² − 2t − 8

	−b		2
tW =		=		= 1 − należy do dziedziny
	2a		2

	1
Więc dla t∊<−1; 1> i dla y=		=> tW = tmax
	y2

	1		1		1
ymax =		=		= −
	tW2 − 2tW − 8		1 − 2 − 8		9

i szukamy min na drugim końcu przedziału

	1		1
y(−1) =		= −
	1+2−8		5

no więc:

	1		1
y∊<−		; −		>
	5		9