nierownosc
P@weł: Witam, mam tu takie zadanko: | x−4 | −
√4x2+8x+4 ≤ 2
Wiem ze prawidlowo zrobiona nierownosc powinna byc sprowadzona do postaci :
| x−4 | −
√(2x+2)2 ≤ 2
| x−4 | − |2x +2| ≤ 2
a mnie zastanawia jednak fakt czy da sie rade zrobic te nierownsc w taki sposob:
| x−4 | −
√4x2+8x+4 ≤ 2
√(x−4)2 −
√4x2+8x+4 ≤ 2 /
2
(x−4)
2 −
√(4x2+8x+4)2 ≤ 4
(x−4)
2 − (4x
2+8x+4) ≤ 4
x
2 − 8x +16 −4x
2 −8x −4 −4 ≤ 0
−3x
2 −16x + 8 ≤ 0
no i tutaj po wyliczeniu delty , pierwiastka z delty, i miejsc zerowych wychodzi brzydki
przedzial , wiec albo cos pomylilem albo ten sposob jest nieprawidlowy

Ktos chetny do
pomocy?
24 kwi 23:20
razor: znasz taki wzór (a−b)
2 = a
2 − 2ab + b
2 ?

właśnie dlatego nie wychodzi
24 kwi 23:22
Anal Iza: Masz blad po podniesieniu stronami do kwadratu.
(a−b)2 = a2−2ab+b2
A Ty po prostu oddzilenie podniosles oba skladniki
24 kwi 23:22
ICSP: Nawet podnieść do kwadratu nie można bez dodatkowych założeń.
Najlepiej rozpisz przedziałami.
24 kwi 23:23
P@weł: no dobra a gdybym jednak sie uparl na ten drugi sposob co napisalem to gdzie mam blad, bo moim
zdaniem dobrze zrobilem, moze ktos mi napisac w ktorym miejscu zle cos napisalem?
24 kwi 23:30
pomocnik: Problem polega na tym, że lewa strona może być ujemna.
Przykładowo:
−4≤1 jest oczywiście prawdą,
a podniesienie obustronne do kwadratu prowadzi do fałszu.
24 kwi 23:33
Mila:
Źle korzystasz z wzorów skróconego mnożenia
| x−4 | − |2x +2| ≤ 2
|x−4|≤|2x+2|+2 i teraz obie strony do kwadratu, bo są nieujemne⇔
(x−4)
2≤(2x+2)
2+4*|2x+2|+4 dalej masz wartość bezwzgledną...
albo trzeba
Przedziałami
albo
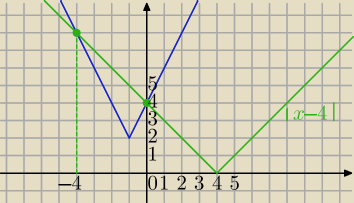
|x−4|<
2+2|x+1| i teraz graficznie,
Wykres g(x)=x−4 leży poniżej wykresu f(x)=
2+2|x+1| dla x≤−4 lub x≥0
24 kwi 23:35
P@weł: Chodzi poprostu o to ze prawidlowo powinieniem podniesc do kwadratu w taki sposob:
√(x−4)2 −
√4x2+8x+4 ≤ 2 /
2
(
√(x−4)2 −
√4x2+8x+4 )
2 ≤ 4
gdzie wedlug wzoru (a−b)
2 a=
√(x−4)2 b=
√4x2+8x+4


?
24 kwi 23:40
Mila:
To też, ale nie możesz podnosić do kwadratu , jeśli nie jesteś pewny , że obie strony
nierówności sa nieujemne.
24 kwi 23:42
P@weł: Dobra, dziękuję bardzo, chyba jednak zostane przy przedziałach

D
24 kwi 23:45
 Ktos chetny do
pomocy?
Ktos chetny do
pomocy?
 właśnie dlatego nie wychodzi
właśnie dlatego nie wychodzi
 Źle korzystasz z wzorów skróconego mnożenia
| x−4 | − |2x +2| ≤ 2
|x−4|≤|2x+2|+2 i teraz obie strony do kwadratu, bo są nieujemne⇔
(x−4)2≤(2x+2)2+4*|2x+2|+4 dalej masz wartość bezwzgledną...
albo trzeba
Przedziałami
albo
|x−4|<2+2|x+1| i teraz graficznie,
Wykres g(x)=x−4 leży poniżej wykresu f(x)=2+2|x+1| dla x≤−4 lub x≥0
Źle korzystasz z wzorów skróconego mnożenia
| x−4 | − |2x +2| ≤ 2
|x−4|≤|2x+2|+2 i teraz obie strony do kwadratu, bo są nieujemne⇔
(x−4)2≤(2x+2)2+4*|2x+2|+4 dalej masz wartość bezwzgledną...
albo trzeba
Przedziałami
albo
|x−4|<2+2|x+1| i teraz graficznie,
Wykres g(x)=x−4 leży poniżej wykresu f(x)=2+2|x+1| dla x≤−4 lub x≥0

 ?
?
 D
D