Ekstrema lokalne Anal Iza: ICSP zajrzyj jak mozesz. Chodzi mi o wyznaczanie ekstremow lokalnych w funkcjach z wartoscia bezwzgledna. Wezmy, np: f(x)=|x²−1| To powinienem rozpisac z definicji wart. bezwzglednej i liczyc 2 pochodne czy jak?

ICSP: Rozpisz przedziałami.

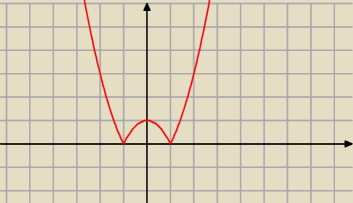
Trivial: Swoją drogą takie zadanie robi się rysując wykres w pamięci. Minima lokalne: x = −1, x = 1 Maksimum lokalne: x = 0.

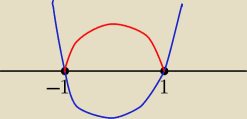
P@weł: Ja na chłopski rozum bym to zrobił tak: x² − 1 Δ= 4 √Δ=2 x₁=−1 x₂=1 rysujemy parabole z ramionami do góry , to co ponizej osi x odbijamy nad poniewaz wartosc bezwzgledna zmienia wartosci ujemne na dodatnie

Anal Iza: f(x) = x² − 1, dla x∊(−∞;−1)∪(1;∞) f(x) = −x²+1, dla x∊(−1;1) I teraz kolejny problem bo pochodne zeruja sie tylko w zerze, a w odpowiedziach mam podane minima w f(−1) i f(1).

Trivial: Do istnienia ekstremum nie jest wymagane istnienie pochodnej.

Anal Iza: Trivial jak ten wykres wyglada i jak narysowac to wiem, ale nie zawsze sa takie latwe funkcje pod modulem(albo cala funkcja jest bardziej skomplikowana). Chce sie nauczyc ogolnego schematu postepowania

Anal Iza: Czyli musze po prostu dodatkowo sprawdzic punkty ktore 'wyrzucilem' przy rozpisywaniu modulu?

Trivial: Musisz do swojego zbioru kandydatów dołożyć punkty −1, 1. Funkcja f jest ciągła, a zatem jeśli pochodna zmienia znak przy przechodzeniu przez te punkty to jest tam ekstremum. Zauważ, że istnienie pochodnej w punkcie nie jest wymagane.

Anal Iza: Ok, czyli jeszcze wypadalo by sprawdzic ciaglosc w tych punktach?

Trivial: Wystarczy zauważyć, że f jest ciągła w R.