planimetria razor: W trójkącie prostokątnym długości przyprostokątnych są równe 6 i 8. Oblicz długość promienia okręgu przechodzącego przez środek krótszej przyprostokątnej i stycznego do przeciwprostokątnej w ich środku. Rozwiązałem to wpisując sobie ten trójkąt do układu współrzędnych, natomiast chciałbym wiedzieć czy da się to rozwiązać bez robienia tego

razor: stycznego do przeciwprostokątnej w jej środku miało być

Saizou : skorzystaj z podobieństwa trójkątów

Saizou : i jak ?

razor: jestem ślepy bo żadnych trójkątów podobnych tu nie widzę http://screenshooter.net/0070634/xqurdye

Saizou : to ja jestem ślepy bo co innego przeczytałem zaraz pomyślę

Maslanek: Masakryczne

Saizou : czemu mi się wydaje że tego jest nieskończenie wiele xd

Maslanek: Może jakby wyjść z pól. Podzielić ten trójkąt na trójkąty prostokątne i jeden prostokąt w rogu przy przyprostokątnych (taki mały ) Ale to tylko jakiś ślad. Nic tu nie widzę Wracam do swojego prawdopodobieństwa

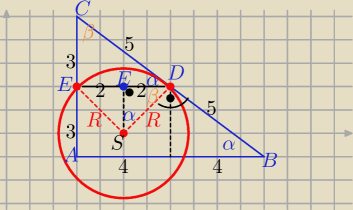
Eta: ................ .......... Trójkąty SDF i ABC są podobne (kkk)

	R		|FD|
		=		⇒ R=.........
	|AB|		|AC|

razor: skąd wiemy że te trójkąty są podobne?

Eta: α+β=90^o |<SDB|=90^o ( bo okrąg styczny do BC to |<SDE|=90^o−α= β zatem trójkąt SFD prostokątny o kątach ostrych α i β ⇒ że jest podobny do ΔABC (kkk)

Saizou : hahaha ale wiedziałem że z trójkątów podobnych

pigor: ..., a ja z tw. o prostej stycznej i siecznej z punktu poza okręgiem z równania 3(3+2R)=5² ⇔ 6R=16 ⇔ R=⁸₃= 2,(6) . ...

Maslanek: To tw. o prostej stycznej i siecznej. Bo wpadło mi do głowy od razu, ale żeby je wykorzystać nie było odległości trzeciego punktu Z jakiego to punktu?

Maslanek: Podbijam

lola: Ja też

Mila: Moi drodzy, uparcie mi wychodzi :

	10
R=
	3

W ΔCED:

	3
sinα=
	5

W ΔSED:

	2
sinα=
	R

2		3
	=		⇔
R		5

3R=10

	10
R=
	3