geometria analityczna Robak: Punkt A=(1,−1) jest wierzchołkiem kwadratu opisanego na okręgu x2 + y2 − 4y − 1 = 0 Znajdź pozostałe wierzchołki tego kwadratu. Mam prostą AS, umiem zrobić to z wektorów, ale nie potrafię tego zrobić z prostej.. niech ktoś mi to wytłumaczy, proszę.

wmboczek: S jest środkiem AC licz prostopadłą do AS przechodzącą przez S znajdź pkt przecięcia prostopadłej z okręgiem

Robak: ale prostopadła do AS to będzie "O" czyli nasze B. I nie widzę tutaj co mi da ten punkt przecięcia?

Robak: ale robię tak jak mówisz więc: Prostopadła do AS przechodząca przez S AS y=−3x+2 Prostopadła do AS

	1
y=		+b
	3x

przechodząca przez S

	1
y=		+2
	3x

Teraz szukam przecięcia prostopadłej z okręgiem.

	1
2√10=x2+(		+2−2)2
	3x

I nie wiem co mi to daje.

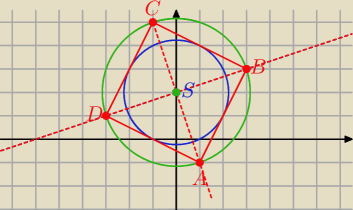
Bogdan: S = (0, 2), A = (1, −1), |AS| = √10,

	1
Prosta AS: y = −3x + 2, prosta DB: y =		x + 2,
	3

okrąg o środku S i promieniu √10: x² + (y −2)² = 10

	1
Rozwiązując układy równań: y =		x + 2 i x2 + (y −2)2 = 10 otrzymamy współrzędne
	3

punktów B i D. Współrzędne C obliczymy korzystając z faktu, że S jest środkiem AC.

Robak: Okrąg ma promień √3 z tego co wyliczyłem. Rozwiązując ten układ równań dla promienia

	27
x2=
	10

i mi to za bardzo nie pasuje na współrzędne..

Robak: Ah dobra widzę, jezu nie zauważyłem tego zielonego okręgu.

Eta: Inny sposób ( z wykorzystaniem własności wektorów) S(0,2) , A (1, −1) → → → AS=[−1,3] i AS=SC ⇒ C(0−1, 2+3) = C(−1,5) wektory AS i BS są prostopadłe i mają równe długości( z własności kwadratu) → → AS=[−1,3] to BS=[3,1] lub BS=[−3,−1] ⇒ [x,y−2]=[3,1] lub [x,y−2]=[−3,−1] zatem x=3 i y=3 lub x=−3 i y=1 ⇒ B(3,3), D(−3,1) co widać na rys. Bogdana