Objętość graniastosłupa prawidłowego trójkątnego jest równa 36p{3}, a pole powie
kamczatka: Objętość graniastosłupa prawidłowego trójkątnego jest równa 36√3, a pole powierzchni bocznej
tego graniastosłupa jest równe 72. Oblicz tangens kąta, jaki tworzy przekątna ściany bocznej z
sąsiednią ścianą boczną.
Mógłby ktoś pomóc ? Bo nawet nie wiem gdzie jest ten kąt.
24 kwi 16:33
kamczatka: ?
24 kwi 17:51
sylwek:
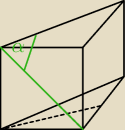
moim zdaniem ten ale nie jestem pewien

24 kwi 18:05
sylwek: z objętości wylicz h lub a potem spróbuj wstawić do pola. to napewno jest potrzebne.
24 kwi 18:12
Marcin:
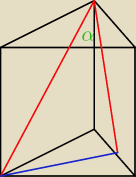
24 kwi 18:36
kamczatka: i teraz wyliczyć a albo h jak napisał sylwek a co dalej ?
24 kwi 18:38
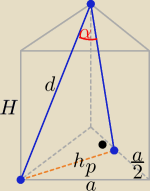
Eta:
24 kwi 18:43
Marcin: No wyznacz sobie H
i podstaw do wzoru na pole boczne.
| | 144 | |
Będziesz mieć |
| *a=24 Policzysz sobie a i H, później już z górki  |
| | a2 | |
24 kwi 18:44
komik: MARCIN możesz jakoś wytłumaczyć dlaczego ten ?
24 kwi 18:45
Marcin: No bo w treści masz podane, że to jest kąt
pomiędzy przekątną ściany bocznej (rysujesz), a
ścianą boczną

Popatrz z resztą na rysunek Ety

24 kwi 18:47
kamczatka:
| 36√3 | | 4 | | 144√3 | |
| = 36√3* |
| = |
| |
| | a2√3 | | a2√3 | |
Dobrze wyznaczyłem H ?
25 kwi 17:56
kamczatka: Dobra już wyszło H = 36 , a = 2
Tylko nie wiem jak obliczyć wysokość sąsiedniej ściany bocznej ?
25 kwi 18:01
kamczatka: bo z pitagorasa wychodzi 362 + 12 = h2
h2 = 1297
dobrze ?
25 kwi 18:02
kamczatka: może ktoś pomóc z wyliczeniem h ?
25 kwi 18:47
dero2005:
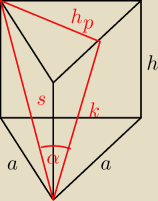
3ah = 72
a = 6
h = 4
k =
√h2 + (a2)2 = 5
25 kwi 19:14
kamczatka: ok dzięki wielkie
25 kwi 19:49
 moim zdaniem ten ale nie jestem pewien
moim zdaniem ten ale nie jestem pewien 



 Popatrz z resztą na rysunek Ety
Popatrz z resztą na rysunek Ety 
