Rozkład wielomianów na czynniki.
OG: Rozkład wielomianów na czynniki.
.64x4−27x7 =
Moje pytanie czy a się to zrobić bez używania wzorów skróconego mnożenia? Gdy po wyłączeniu x
przed nawias w nawiasie pozostaje równanie kwadratowe, można uzyskać ładny wynik deltą. W tym
przypadku takiego równania kwadratowego nie ma.
24 kwi 15:16
ICSP: Można użyć wzorów na pierwiastki równania sześciennego.
24 kwi 15:19
J: = 64x4(1 − 27x3)
24 kwi 15:19
J: Sorry... = x4(64 − 27x3)
24 kwi 15:20
J:
| | 64 | | 4 | | 4 | |
64 − 27x3 = 0 ⇔ x3 = |
| ⇔ x = |
| lub x = − |
| |
| | 27 | | 3 | | 3 | |
24 kwi 15:23
zawodus: 64−27x3=43−(3x)3=...
24 kwi 15:23
ICSP: Witaj
zawodus 
Pytanie mam

24 kwi 15:31
zawodus: [C[ICSP] witaj

boję się, ale dawaj

24 kwi 15:39
24 kwi 15:40
ICSP: Mam obliczyć odległość między przekątnymi sąsiednich ścian sześcianu nie wychodzącymi z jednego
wierzchołka. Przyjmijmy, że sześcian ma krawędź jednostkową.
Jakieś pomysły ?

24 kwi 15:41
zawodus: czekaj kiedyś robiłem coś takiego

muszę zrobić rysunka

24 kwi 15:43
ICSP:
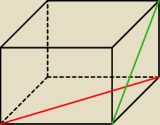
24 kwi 15:48
zawodus: Na pewno jeden sposób to analityczny umieścić sześcian w R3 i badać odległość między prostymi

Ja jednak szukam czegoś na płaszczyźnie

24 kwi 15:49
ICSP: ale własnie jak znaleźć tą odległość

24 kwi 15:50
zawodus: Na odległość między prostym w R
3 jest gotowy wzór

24 kwi 15:54
ICSP: Pierwszy raz o tym słyszę

24 kwi 15:59
24 kwi 16:06
ICSP: hmm, jakoś nie widzę tutaj równoległościanu

24 kwi 16:10
zawodus: na stronie 95 jest wzór tylko trzeba go rozszyfrować

24 kwi 16:21
zawodus: ewentualnie piszemy równania płaszczyzn równoległych zawierających owe proste i badamy
odległość między nimi

24 kwi 16:29
ICSP: Tylko ja nie widzę w tym zadaniu równoległościanu

Z obliczeniami sobie bez problemu poradzę.
24 kwi 16:32
zawodus: Obliczyłem, że gdy a=3 to odległość wynosi
√3 
24 kwi 16:51
 Pytanie mam
Pytanie mam 
 boję się, ale dawaj
boję się, ale dawaj 


 muszę zrobić rysunka
muszę zrobić rysunka 

 Ja jednak szukam czegoś na płaszczyźnie
Ja jednak szukam czegoś na płaszczyźnie 



 Tylko trzeba doczytać wcześniej, żeby oznaczenia kojarzyć
Tylko trzeba doczytać wcześniej, żeby oznaczenia kojarzyć  https://www.google.pl/url?q=http://home.agh.edu.pl/~gora/algebra/Wyklad13.pdf&sa=U&ei=JRlZU72XHerE4gSD84DwAg&ved=0CCsQFjAC&sig2=vso19vpqowani0X5n-_1WQ&usg=AFQjCNGq7cREOGkRbMysMb_MJu_8xK1dcw
https://www.google.pl/url?q=http://home.agh.edu.pl/~gora/algebra/Wyklad13.pdf&sa=U&ei=JRlZU72XHerE4gSD84DwAg&ved=0CCsQFjAC&sig2=vso19vpqowani0X5n-_1WQ&usg=AFQjCNGq7cREOGkRbMysMb_MJu_8xK1dcw



 Z obliczeniami sobie bez problemu poradzę.
Z obliczeniami sobie bez problemu poradzę.
