Geo analityczna Marcinek : Dany jest trójkąt ABC, gdzie A=(−2,−1), wektor AB=[8,4] a punkt przecięcia środkowych X=(1,4). Znajdź pozostałe wierzchołki trójkąta. B wyliczam bez problemu jest to (6,3) potem środek odcinka AB czyli D=(2,1) odległość środka AB od punktu przecięcia sie środkowych (S) wychodzi mi √10 , więc odległość od trzeciego punktu jest równa 3√10. Następnie wyliczam prostą przechodzącą przez środek AB i punkt S , wychodzi mi y=−3x+7 , więc szukany punkt jest postaci (x,−3x+7) próbuje więc ze wzoru na odległość punktu D od C √(2−x)² + (1−(−3x+7))² = 3√10 . no i tu jest problem bo za nic nie może mi wyjść dobry wynik , co robię źle ? a może jakiś prostszy sposób ?

loitzl9006: można prościej, wykorzystując wzór na współrzędne środka ciężkości Δ ABC (jest w tablicach) środek ciężkości ΔABC − punkt przecięcia środkowych w tym ΔABC:

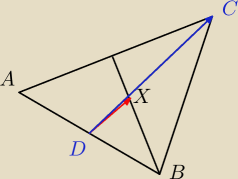
zawodus: masz A i wektor AB ⇒ masz też B D policzyłeś

	1
wystarczy skorzystać z faktu, że DX→=		DC→
	3

zawodus: Ja podałem inny sposób, żeby mógł wykorzystać swój policzony punkt D

Marcinek : nie lubię wektorów ale dzięki udało mi się w końcu