aa Hugo: Dla jakich wartości parametru m równanie sin²x +sinx +m=0 sin²x +sinx +m=0 t:=sinx t²+t+m=0 Δ≥0 Δ=t²+t+m≥0 1−4m≥0 0,25≥m

J: Co równanie ... ?

Hugo: czytam rozw i pisze mi też że gdy g(1)>= 0 ⇔ 1+1+m>=0 Ale skąd to sie bierze g(1)>=0

Hugo: ...ma rozwiązanie //Wybacz

J: Jaka jest treść zadania ?

J: To,że delta jest nieujemna dopiero gwarantuje pierwiastki t , ale musi być jeszcze spełniony warunek: − 1 < t < 1

J: Ściślej ... − 1 ≤ t ≤ 1

Hugo: oglądam sb wywiady z gimbą o teście z matmy... EPIC !

Hugo: okej J... myśle myśle...

Hugo: a gdyby sb policzyć g(−1) i g(1)? i nam wyjdzie ?

Hugo: g(1)= sin²x +sinx +m=0 sin²1 + sin1+m=0 1² + 1+m=0 m=2 g(−1)=sin²x +sinx +m=0 sin²−1 + sin−1+m=0 korzystamy z wzorów redukcyjnych −sin² + −sin1+m=0 1−1+m=0 m=0 //// czy dobrze to zapisałem ? chodzimy o wyrzucenie minusa przed kwadrat sinusa

Hugo: zatem 0≤t≤1 0≤sinx≤1 oraz drugie założenie m≤1/4 daje nam me<0;1/4> i taka ma być odp.. czy wszystko dobrze Q: skąd inspiracja na nick J?

J: Aby t spełniało warunki to x_w musi leżeć pomiędzy −1 i 1 oraz g(−1) >0 i g(1) > 0

J: Chodzi oczywiście o x_w dla nierówności: t² + t + m ≥ 0

Hugo: g(−1) ≥ 0 i g(1) ≥ 0? Ale oczywiście dz rozumiem... Wiesz to boli wiesz niby wszystko a nie umiesz zadanie ;x A wracając jeszcze tiam jedno... sin²(−1) = −sin² czy to jest dobrze zapisane i się równa 1?

J: Argumentem funkcji trygonometrycznych jest kąt ( w stopniach lub radianach). Co u Ciebie oznacza: sin(−1) ?

Hugo: w sumie to tam mam błąd ehmm al ei tak dobrze wychodzi 8) g(−1) −> m>=0 g(1) −> m>=−2 m>=0

Hugo: sin od −1.. bo jak podstawiałem pod g(−1) musiałem dać pod x =−1 czyli sin(−1) i wyrzucamy minus przed nawias −sin(1) .... ale tam miałem kwadrat sin²(−1) co nam daje −sin²(1) =1 czy tak

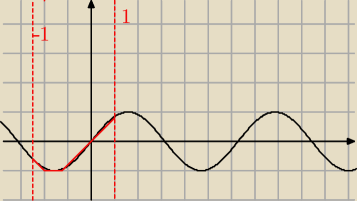
Hugo: W sumie łudze sie że lepiej było to narysować po prostu

J: Chyba jednak do konca nie rozumiesz.. skoro stosujesz podstawienie sinx = t , to na t nakładasz warunek − 1 ≤ t ≤ 1 ( bo sinus ma tylko wartości w tym przedziale. Aby to uzyskać, musi być dla równania g(t) warunek: x_w ∊ (−1,1) i g(−1)>0 i g(1)>0.. te trzy warunki gwarantują,że − 1 < t < 1

Hugo: //dobra ostatnie i lecimy arkusze Znajdz te wartości parametru m dla których równanie (1−sinx)m²+2m+4sinx −8=0 ma rozwiązanie równanie kwadratowe => Δ≥0 sinx e<−1,1> (1−sinx)=/=0 ⇔ sinx≠1 ⇔ sinx≠3/2pi +2kpi (1−sinx)m²+2m+4sinx −8=0 Δ_m=4−4(1−sinx)(4sinx −8) Δ_m=4−4(−4sin²x + 4sinx −8 +8) Δ_m=4+ 16sin²x − 16sinx 4+ 16sin²x − 16sinx ≥0 1+ 4sin²x − 4sinx ≥0 sinx=:t t² −4t+4≥0 //////////// miałem tu chwile zwątpienie bo zgubiłem b²−4ac Δ_t=16−16=0 (t−2)²>=0 t=2 Parambooooola ♥ te<2; oo) sinx e (−oo ;2)> U sinx e <2 ; oo) => sinx e R sprzeczne ;>? oraz sinx e <−1;1> zatem sinx e <−1;1>? => dla m e <−1;1>? + dziedzina sinx=/=1 => m e <−1;1)

zawodus: Totalna bzdura Mylisz parametr ze zmienną

zawodus: (1−sinx)m²+2m+4sinx−8=0 m²−m²sinx+2m+4sinx−8=0 sinx(4−m²)=8−2m−m² sprawdzam co się dzieje dla m=2 i m=−2 (tutaj będzie ewentualnie jakaś odpowiedź) zakładam, że m≠−2 i m≠2 i dzielę przez 4−m²

	8−2m−m2
sinx=
	4−m2

teraz równanie ma rozwiązanie, gdy:

	8−2m−m2
−1≤		≤1
	4−m2

Hugo: :............: dzięki zawodus....

	8−2m−m2
−1≤
	4−m2

z założeniami mnożymy −4+m²≤ 8−2m−m² −4+2m²−8+2m≤0 2m²−12+2m≤0 m²−6+m≤0 Δ? Δ= 1+6*4=21

	8−2m−m2
1≤
	4−m2

4−m²≤ 8−2m−m² 4 ≤ 8−2m −4≤−2m m≤2

ICSP: 6*4 = 20 ?

ZKS: Masz nierówność wymierną a Ty sobie mnożysz od tak przez ten mianownik. Dalej również jest błąd 1 ≥ ...

ICSP: i podaj dziedzinę do nierówności :

	8 − 2m − m2
−1 ≤
	4 − m2

Hugo:

	8−2m−m2
−1 ≤
	4−m2

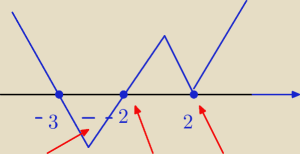
Dziedzina: 4−m² =/=0 m≠ 2 v m≠ −2 Czyli sprowadzamy do wspólnego mianownika?

	8−2m−m2		4−m2
0≤		+
	4−m2		4−m2

	8−2m−m2+4−m2
0≤
	4−m2

	12 −2m −2m2
0≤
	4−m2

pomocnicza delta? 12 −2m −2m²=0 /:2 Δ= 6 −m−m² Δ=1+24

	1−5		1+5
m1=		v m2=
	−2		−2

m₁=2 v m₂=−3 Znak ilorazu jest taki sam jak znak iloczynu 0≤(m−2)(m+3)(4−m²) 0≤(m−2)(m+3)(m−2)(m+2) 0≤(m−2)²(m+3)(m+2) wężyk? me <−3;−2> U {2}

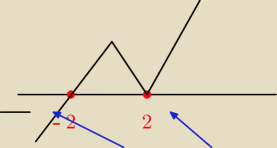
Hugo: TAM MAM ŹLE post wyżej policzyłem dla ≥ tam sie m e (−oo ;−3> U <−2; oo)

	8−2m−m2
1≥
	4−m2

	8−2m−m2		4−m2
0≥		−
	4−m2		4−m2

	8−2m−m2− 4+ m2
0≥
	4−m2

	4−2m
0≥
	4−m2

Znak ilorazu jest taki sam jak znak iloczynu 0≥(4−2m)(4−m²) x=2 v x = 2 v x=−2 wężyk me (−oo; −2> u {2}

Hugo: Suma me (−oo; −2> u {2} m e (−oo ;−3> U <−2; oo) założenia: m≠{−2,2} me (−oo −2) co mam tu źle bo pewnie znowu coś mam

Hugo: .

Hugo: dobrze to mam ?