Zadanko 5-latek: czescDraghan Znalazlem dla Ciebie ciekawe zadanko z planimerii . Niech h bedzie dlugoscia wysokosci trojkata prostokatnego opuszczonej z wierzcholka kąta prostego a r dlugoscia promienoa okregu wpisanego w ten trojkat . Udowodnic ze

	h
2<		<=1+√2 orz z etych szacowan nie mozna poprawic . Przynajmniej to
	r

	h
2<
	r

bezendu: 5−latek daj chłopakowi jakieś maturalne, bo tę to wgl nawet koło matury to nie leżały

5-latek: czesc bezendu To jest maturalne zadanie .

bezendu: Witam, ale chyba z 1980 albo jeszcze starsze

Eta: 1968

bezendu: Witaj Eta kończymy dziś tą planimetrię ?

5-latek: Powitalem juz Cie w iinym poscie Chyba tak bedzie jak piszsesz bo ja to mam z 1976r (mam taki zbior .

5-latek: A dla Ciebie bezendu takie proste dane sa punkty A(2,1) B(−3,2) i C( 2m−1),(1−m) Dla jakich wartosci m sa one wierzcholkami teojkata a) ostrokatnego b) prostokatnego i c) rozwartokatnego .?

bezendu: Za dużo liczenia ale trzeba sprawdzać warunki |AB|²+|BC|²=|CB|² Rozwarty: |CB|²>|AB|²+|AC|² |CB|²<|AB|²+|AC|² ostrokątny To zadania z analitycznej, a z tym działem problemów nie mam

Piotr 10: A ktory bok to najdluzszy ?, bo wg mnie to trzeba do kazdego podpunktu 3 przypadki rozwazyc

bezendu: No tak ja zrobiłem jeden przypadek.

5-latek: Pewnie ze proste do a) warunek zadania to ABoAC>0 i BAoBC>0 i CAoCB>0 (sa to wektory do b) warunek zadania jest rownowazny warunkom 1.Wektor Ba jest nierownolegly do BC i ( ABoAC=0 lub BAoBC=0 lub CAoCB=0) ( to sa wektory )

	2+2m		−1−m
ale tez 2. ale tez wektor BA jest rownolegly do BC wtw		=		wtw m=−1wtw
	5		−1

BC=o(te ostatnie to wektory) o ze strzalka na gorze to wektor zerowy do c) warunek zadanka jest rownawany warunkom (ABoAC<0 lub BAoBC<0 lub CAoCB<0) (sa to wektory

5-latek: Ja pisalem a Wy juz sobie wyjasniliscie

zawodus: A co z tym pierwszym?

bezendu: Odpoczywa sobie

Piotr 10: bezendu hehe .

5-latek: Czesc. Zaciekawilo CIe ? Niech ab to dlugosci przyprostokatnych i c −dlugosc przeciwprostokatnej trojakta

	1		1
Ptr= 12ab=		ch=		(a+b+c)
	2		2

	a+b		a*b		h		a+b+c		a+b
Z tego h=		i r=				=		= 1+
	c		a+b+c		r		c		c

Z wlasnosci odleglosci mamu ze a+b>c oraz ze a+b≤c√2 bo dla liczb ai b (a−b)²≥0⇔(a²+b²≥2ab⇔c²≥2ab⇔2c²≥(a+b)²⇔c√2≥a+b

	h		a+b
to 2<		=1+		≤1+√2
	r		c

	h		h
Teraz gdy a=b to		= 1+√2 , natomiast gdy ustalimy b to lim a→0		=2
	r		r

5-latek: Tak naprawde to jestem zmeczony bo wczoraj przerzucilem chyba ze 6 ton papieru Papier wcale nie jest lekki jak by sie wydawalo

bezendu: Bardzo maturalne.... Od kiedy nas obowiązuję granice ?

zawodus: ostatni fragment trochę nie maturalny Powinno być

	ab
h=
	c

5-latek: bezendu wiem ze nie maacie teraz granic ale napisalem rozwiazanie calego zadanka. MOze CI sie kiedys przydac

	a*b
oczywiscie ze ma byc h=		. DObrze ze to zauwazyles Ale jak sie piszse to takie
	c

wredne chochliki sie zdarzaja

staszic: Witam was serdecznie

zawodus: witojcie

staszic: Może rozwiazemy jakiś dowód z planimetrii?

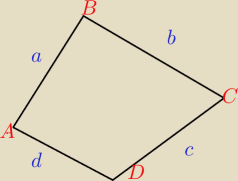
5-latek: Bezendu . A moze sprobujesz takie zadanko . Nie matrw sie jesli nie zrobisz . Spokojnie Czy istnieje taki czworokat ABCD ktorego dlugosci bokow spelnialyby uklad 3 warunkow 1. AB<CD<AD<BC 2. AB+BC=CD+DA 3. AB²+BC²=CD²+DA² Mozesz to zrobic geometrycznie lub algebraicznie . jak chcesz Algebraicznie to moze dwie linijki

5-latek: Jesli CI bezendu pozwoli to akuratnie masz

staszic: Skąd to zadanie wziales?

Piotr 10: 2/ Dlugosci ramion trapezu opisanego na okregu sa rowne c=4 , d=8. Środkowa trapezu dzieli go na dwa trapezy z ktorych mniejszy ma pole trzy razy mniejsze od pola danego trapezu. Wyznacz dlugosci podstaw danego trapezu.

staszic: Twierdzenie o kątach w czworokącie.

5-latek: To napisze rozwiazanie zadania z 13:02 (moze sie komus przyda Algebraicznie Z warunku nr 3 mamy (a−c)(a+c)= (d−b)(d+b) Z warunku nr 2 i uwzgledniajac warunek nr 1 to widzimy ze a−c=d−b≠0 A wiec a+c=d+b co z warunkiem nr 2 daje a=d co jesst wbrew zalozeniu nr 1 Wic nie istniej taki czworokat ktory by spelnial dany uklad warunkow .

Draghan: Witaj 5−latek i witajcie wszyscy pozostali Heh, tu już − widzę − pozamiatane Ale tego pierwszego to bym nie zrobił

zawodus: Jestem ciekaw rozwiązania graficznego, bo algebraicznie to łatwo

5-latek: Wiem ze trudne i takiego nie bedzie na maturze . Sprobuj wykazac geometrycznie to z 13:02 . jak wroce z pracy to napiszse rozwiazanie . I zadanko tez mysle ze bedzie dla Ciebie akurat Tresc : Obliczyc dlugosci a b c bokow trojkata prostokatnego ABC wiedzac ze liczby a b i c sa liczbami calkowitymi , i pole trojakta jest rowne obwodowi trojkata .

Piotr 10: A moje zadanie ?

Draghan: Ja geometrycznie na bank nie zrobię, bo wiem, że nie umiem Ale to z 13.41 wydaje się przyjazne Może nawet coś uda się policzyć

5-latek: Zawodus . Te zadanka sa z tego zbioru zadan co pokazywalem CI w linku z allegro . Geometrycznie to napiszse kolo 23 jak wroce z pracy . Dzisiaj sie lepiej czuje i wydaje mi sie ze z godzine po pracy posiedze na forum . I napiszse rozwiazania . Post z 13:41 byl oczywiscie do Draghana

5-latek: Piotr10 to naciskaj kolegow maturzystow Niech sie wykażą.

Piotr 10: 5−latek słoneczko jest, więc nie będzie naciskał

5-latek: A u mnie pewnie zaraz bedzie burza (cos tak sie zanosi Byle wytrzymalo do 14:30 (bede juz w samochodzie

Draghan: Trzeba być dobrej myśli U mnie zanosi się na deszcz. Jak codziennie tutaj

zawodus: Muszę sobie konto w banku doładować i kupić w końcu parę książek

zawodus: Piękne to zadanie Są tylko dwa takie trójkąty

Draghan: Heh Ja zapisałem całą stronę A4 dwoma równaniami i jakoś mi nie wychodzi ani jeden XD Ale zadanko rzeczywiście wygląda ładnie

Draghan: Mam że a²b² − 4a²b − 4ab² + 8ab = 0 Jestem gdzieś na właściwej ścieżce?

cs: Draghan żaden wzór na pole trójkata nie kojarzy ci się z połową obwodu

zawodus: Draghan na właściwej Nie wiem czy najkrótszej, ale prowadzącej do celu

Draghan: Kojarzyć, to się kojarzy, cs Trochę tych wzorów na pole trójkąta jednak jest, a ja nie lubię się bawić z pierwiastkiem To wziąłem "klasyczny" wzór Dzięki, zawodus Ale czy coś dalej z tym zrobię, to już inna sprawa xD

zawodus: Wskazówka Rozwiązać równanie w liczbach całkowitych (a nawet naturalnych)

zawodus: Jak tam wynik?

bezendu: 0:0

Marcin: Jednym z takich trójkątów, jest trójkąt pitagorejski 5,12,13.

zawodus: dobrze wszystkie są Pitagorejskie

Marcin:

Draghan: Eeee... Zapomniałem o tym. Zacząłem robić maj 2010, potem co innego jeszcze... Ale i tak nie wiem, jak ruszyć dalej tamto równanie.

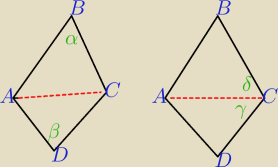
5-latek: Wiec jestem juz i dowod geometryczny do czworokata AB=a BC=b CD=c i DA=d i kąt ABC= α i kąt CDA=β Zwarunkow 2 i 3 mamy ze ab=cd Z tweirdzenia cosinusow jest AC²=a²+b²−2abcosα rowniez AC²=c²+d²−2cdcosβ Zatem po uwzgledniu warunku 3 i tego z e ab=cd wynika ze α=β Wiec ze wzoru na pole trojkata (tego z kątem mamy ze P_trABC=P_trACD wobec czego wbrew warunkowi nr 1 te trojkaty bylyby przystajace Oznaczymy kąt ACB=δ i kat DCA=γ to z tweierdzenia sinusow i waarunku nr 2 mamy sin(pi−γ−α)+ sinγ=sin(pi−α−δ)+sinδ

	α+2δ		α+2γ
Wiec z tego sin		= sin		a wiec δ=γ lub δ=pi−α−γ
	2		2

czyli kąt ACB= kątowi ACD lub kat ACD= kątowi CAD

5-latek: Czesc Draghan Rozwiazanie do zadanka z godziny 13:41 promien okregu wpisanego w ten trojkat ma dlugosc 2 (policz to sobie to c=a+b−4 Warunki zadania {a+b−4=c {a²+b²=c²

	ab
z tego a+b−2=
	4

Musimy zauwazyc ze liczby a i b musza byc parzyste lub jedna z nich musi byc wielokrotnoscia liczby 4− bo inaczej iloczyn ab bylby liczba niepodzielna przez 4 1. niech a=2k b=2s k is liczby naturalne rozne od 0 i wtedy 2k+2s−2=ks

	2
ale s nie rowna sie 2 wiec		=k−2
	s−2

stad mamy s−2=1 lub s−2=2 lub s−2=−1 lub s−2=−2 W przypadku 1 s=3 i k=4 wiec a=8 b=6 c=10 W przypadku drugim s=4 k=3 wiec a=6 b=8 c=10. Nastepne przypadki nie moga zachodzic bo byloby s=0 lubk=0 (a to wbrew zalozeniom 2. Niech a=4k i k liczba naturalna wtedy mamy 4k+b−2=kb Musimy przy tym zauwazyc ze b nie rowna sie 4 wiec

	2
k=1+		stad mamy
	b−4

b−4=1 lub b−4=2 a wiec b=5 a= 12 c= 13 lub b=6 a=8 c=10 A poniewaz kazdy z tych trojaktow jest trojkatem prostokatnym (Wykorzystakj tweiedzenie odwrotne do Pitagorasa) wiec sa one jedynymi trojalatami dla tego zadanka

Draghan:

Witaj, 5−latek Dla Ciebie beczka z jabłuszkami

5-latek: Bardzo dziekuje czy byly ciekawe takie zadanka

5-latek: W sobote jak wroce od brata (po poludniu to wrzuce CI jeszce ale z algebry jakie ciekawe

Draghan: Tak, były ciekawe Dzięki bardzo

zawodus: Draghan rozwiąż to równanie a²b² − 4a²b − 4ab² + 8ab = 0

Draghan: Ale wydaje mi się, że nie umiem. Mam równanie z dwiema zmiennymi. Wyłączyć coś przed nawias? Potraktować wzorami skróconego mnożenia?

zawodus: wyłącz przed nawias ab

zawodus: jakieś postępy?

Draghan: Dziękuję, wyłączyłem Zastanawiam się, co dalej Ale nie chciałbym podpowiedzi, muszę sam na to wpaść

zawodus: dobra to zadanie wstępne Wyznacz wszystkie liczby naturalne x i y spełniające dane równanie: xy=7+y+x Zrób najpierw to

Draghan:

zawodus: dobrze to ja ci pokażę jak zrobić zadanie wstępne xy=7+y+x xy−y=7+x y(x−1)=7+x najpierw co się dzieje, gdy x=1 dostajemy 0=8 No to teraz dzielimy

	7+x		x−1+8		8
y=		=		=1+
	x−1		x−1		x−1

	8
Teraz wystarczy, aby ułamek		był liczbą naturalną
	x−1

To już banał Jedyne naturalne rozwiązania to (2,9),(9,2),(3,5),(5,3) Draghan To zadanie jest dla gimnazjalistów

Draghan: −.− Dziękuję

zawodus: teraz ty kończysz zadanie poprzednie wskazaną metodą

Draghan: ab −4a −4b +8 = 0 ab −4a = 4b −8 a(b−4) = 4b −8 Tutaj ni wim, ale wydaje mi się, żeby sprawdzić co będzie, kiedy (b−4) się wyzeruje... 0a = 16−8 0a = 8 Dalej...

	4b −8
a =		Szczerze, to nie mogę wpaść na to, jak to uprościć, więc wstawiam sobie do
	b −4

tego liczby. Równanie spełniają liczby {a=2, b=0}, {a=0,b=2}, {a=8,b=6}, , {a=6,b=8}, {a=5,b=12}, {a=12,b=5}.

zawodus:

	4(b−4)+8		8
a=		=4+
	b−4		b−4

Draghan: Nie chcę mojego nieogaru zwalać na pogodę, ale coś w tym musi być. Okropnie niskie ciśnienie, ja po dwóch kawach a oczy dalej się zamykają Chyba nici będą z dzisiejszego liczenia. Dziękuję po raz kolejny