nierownosc P@weł: Witam , mam zadnie z nierówności i mam co do niego pytanie , oto one:

	2x−3
|		| ≥ 2
	x2−1

Rozbijam na 2 możliwosci: 1^o x≥2 v 2^o x≤ −2 1^o x≥2

2x−3
	−2 ≥ 0 dziedzina:
x2−1

x²−1 ≠0 (−2x² + 2x −1)(x²−1) x≠−1 x≠1 brak x₁=−1 x₂=1 pierwiastkow Wykres dla pierwszej mozliwosci wyszedl jak na rysunku Czyli przedzial to : x∊(−1,1) I tu sie zastanawiam czy oby przedzial byl prawidlowy, czy tutaj dla tego przedzialu x∊(−1,1) uwzględniam x≥2 Czyli ma byc x∊∅ juz sam nie wiem, niech ktos podpowie

P@weł: ?

P@weł: Prosze o pomoc

P@weł: ?

Tadeusz: ... NIE MA TAKICH WARUNKÓW ! Skąd Ty bierzesz to x≤2 ∨ x≤−2 ?

Tadeusz:

	2x−3
|		|≥2 rozpisujesz na:
	x2−1

2x−3		2x−3
	≤−2 ∨		≥2 i tym się bawisz−
x2−1		x2−1

P@weł: To jak inaczej rozwiazac te nierownosc?

	2x−3		2x−3
jak nie tym sposobem:		≥ 2 v		≤−2
	x2−1		x2−1

P@weł: To po jakiego H... korepetytor mi tak tlumaczyl...

Tadeusz: ... no tym. Jedną już rozwiązałeś tylko sam zwątpiłeś i "uparłeś" się uwzględniać x≥2 −

Tadeusz: Pewnie dobrze tłumaczył tylko Ty kręcisz to nie x≤−2 ∨ x≥2 tylko ≤−2 ∨ ≥2

	2x−3
a to
	x2−1

P@weł: sorry za slowa, nie moglem sie postrzymac.. Tadeuszu moglbys mi szybko sprawdzic czy dobrze zrobilem zadanie? ::

	2x−3
|		| ≥2
	x2−1

2x−3		2x−3
	≥2 v |		| ≤−2
x2−1		x2−1

1^o

2x−3
	≥2
x2−1

dziedzina (−2x²+2x−1)(x²−1)≥0 x∊R\{−1,1} brak x₁=−1 x₂=1 pierwiastkow x∊−1,1) 2^o

2x−3
	≤−2
x2−1

(2x²+2x−5)(x²−1)≤0 dziedzina x∊R\{−1,1}

	−1−√11
x1=
	2

	−1+√11
x2=
	2

x₃=−1 x₄= 1

	−1−√11		−1+√11
x∊<		, −1 ) ∪ (1 ,		>
	2		2

Odp: Suma przedziaøów z warunkow 1^o i 2^o:

	−1−√11		−1+√11
x∊ <		, −1 ) ∪ (−1,1) ∪ (1 ,		>
	2		2

P@weł: ?

Tadeusz: wygląda, że OK

P@weł: Bylbyym wdzieczny gdybys sprawdzil mi jeszcze jedno podobne zadanie, zaraz tutaj napiszé

Tadeusz: − jeśli jeszcze będę

P@weł:

4−x		1
	>
x−5		1 − |x|

No i tutaj tez nie wiem czy moge napisac tak jak we wczesniejszej nierownosci : 1^o x≥0 v 2^o x<0 1^o

4−x		1
	>
x−5		1 − x

4−x		1
	−		> 0
x−5		1−x

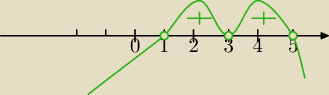
(x² −6x +9)(x−5)(1−x) > 0 dziedzina x₁= 3 x₂=5 x₃=1 x∊R\{1,5} pierwiastek podwojny Rysunek: 1 Patrz rysunek No i sie zastanawiam nad przedzialem czy będzie: x∊(−∞,1)∪(5,∞) czy Uwzględniając x≥0 będzie : x∊ <0,1)∪(5,∞) Móglbyś sobie te nierownosc rozpisac, zobaczyc czy dobrze robie?

P@weł: ?

P@weł: ?

Tadeusz: tutaj oczywiście ... pod modułem jest x i rozpatrujesz jak należy − ALE ... −

Mila: Dziedzina : x≠5 i |x|≠1 x≠5 i x≠1 i x≠−1 (x² −6x +9)(x−5)(1−x) > 0 ⇔ (x−3)²*(x−5)*(1−x)>0 x∊(1,3)∪(3,5) rozwiąż dla x<0

4−x		1
	>
x−5		1+x

Tadeusz: (x² −6x +9)(x−5)(1−x) > 0 −(x−3)²(x−5)(x−1)>0 czyli zaczynasz od dołu albo: (x−3)²(x−5)(x−1)<0 i rysujesz od góry

P@weł: Moglbys sobie na karteczce szybko rozwiazaac te nierownosc, bo piszac tutaj wiecej tobie czasu zajmie, chcialbym abys mi podal prawidlowa odpowiedz, bo ja to robilem na dwa sposoby no i wychodza mi dwie inne odpowiedzi. Bym rozpisal moje dwie wersje ale nie wiem czy masz na to tyle czasu

P@weł: Ok rozwiazuje dla x<0

P@weł: x<0

4−x		1
	>
x−5		1 + x

4−x		1
	−		> 0
x−5		1 + x

(4−x)(x+1) −(x−5)
	> 0 / ( (x−5)(1 + x) )2
(x−5)(1 + x)

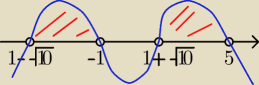
( (4−x)(x+1) −(x−5) )(x−5)(1 + x) > 0 (4x + 4 −x² −x −x +5 )(x−5)(1 + x) >0 (−x² +2x +9)(x−5)(1 + x) >0 √Δ=√40= 2√10 x₃=5 x₄= −1 x₁= 1+√10 x₂= 1−√10 Rysunek x∊(1−√10, −1) ∪ (1+√10 , 5)

Mila: x∊(1−√10, −1) ∪ (1+√10 , 5) i x<0 więc odrzucasz przedział z dodatniej części osi x∊(1−√10, −1) odp.x∊(1−√10, −1)∪(1,3)∪(3,5)

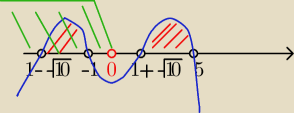
P@weł: No i co Mila ja mam u siebie w wyżej napisanym przedziale tzn : x∊(1−√10,−1)∪(1+√10,5) uwzglednic x<0 , czyli ma byc poprawnie: x∊( 1−√10 , −1 ) tak jak na rysunku: (patrz rysunek)

P@weł: A w 1^o Warunku przedzial jest caly tzn : x∊(1,3)∪(3,5) gdyz x≥0 pokrywa go calego dlatego przepisujemy w calosci, prawda?

Mila: Zgadza się.

P@weł: Mila będę wdzieczny jesli jeszcze mi cos sprawdzisz, zaraz napiszę:

P@weł: Chodzi glownie o pierwszy warunek, chcę rozpisac go na 2 sposoby, no i nie wiem ktory jest poprawny , albo,gdzie robię błąd :

4−x		1
	>
x−5		1−|x|

1^o x≥0 I sposób

4−x		1
	−		> 0
x−5		1−x

4−x		1
	−		> 0
x−5		−(x−1)

(x−1)(4−x) + 1(x−5)
	> 0 / * ((x−5)(x−1))2 dziedzina
(x−5)(x−1)

D: X∊R\{1,5} (4x−x² − 4 +x +x −5)(x−5)(x−1) > 0 (−x² +6x − 9)(x−5)(x−1) > 0 x₁=3 x₂=5 x₃=1 pierwiastek podwojny Według I sposobu wychodzi przedział x∊(1,3)∪(3,5) II Sposób dla x≥0

4−x		1
	−		> 0
x−5		1−x

(4−x)(1−x) −(x−5)
	>0 /* ((x−5)(1−x))2
(x−5)(1−x)

((4−x)(1−x) −(x−5))(x−5)(1−x) > 0 Dziedzina x∊R\{1,5} (4−4x−x+x²−x+5)(x−5)(1−x) >0 (x² −6x + 9)(x−5)(1−x) >0 x₁=3 x₂=5 x₃=1 pierwiastek podwojny No i tutaj w II Sposobie wychodzi mi ze przedzialem jest , uwzgledniajac x≥0: x∊<0,1) u (5,∞) Wiec który jest poprawny

P@weł: ?

Tadeusz: ... przecież pokazałem Ci to w poście z 20:55 ... patrz to co na czerwono

P@weł: Czyli gdybym zrobil I Sposobem wyszedl by mi koncowy wynik(suma): x∊(1−√10, −1)∪(1,3)∪(3,5) A gdybym zrobil II spobobem Wynikiem koncowym rownania bylo by: x∊(1−√10, −1)∪<0,1)∪(5,∞) Czyli ogolnie nierownosc ta moze miec dwa rozwiązania , zalezne od Sposobów Rozwiązania?

P@weł: ?

Mila: Tadeusz juz Ci wyjaśniał. No to jeszcze raz: (x² −6x + 9)(x−5)(1−x) >0 to jest dobrze. ⇔(x−3)²*(x−5)*(1−x)>0 (x−5)*(1−x) parabola skierowana w dół. Zaczynasz rysoważ wężownicę od dołu. Tam we wpisie tak Ci pokazałam 20:54. Popraw dziedzinę, zapominasz wyłączyć (−1).

P@weł: Mila juz znalazlem bład w tym II sposobie ktory napisalem jest: (x² −6x + 9)(x−5)(1−x) >0 czyli wspolczynnik a przy najwyzszej potedze jest ujemny i ramiona rysujemy od dołu, dzieki bardzo nie zauwazylem tego wczesniej Dziękuję wam za pomoc

Mila: To pięknie, że już wszystko wyjaśnione.

P@weł: Dziedzina moim zdaniem jest poprawnie, bynajmniej nie mam zastrzezen

Mila: D: x−5≠0 i 1−|x|≠0⇔ x≠5 i x≠1 i x≠−1 D=R\{−1,1,5}

P@weł: yhym racja, rozzwiazywalas dziedzine juz na samym poczatku, nie zauwazylem tego , dziekuję!

Mila: