punkt leżący w płaszczyźnie kąta maturzysta: Wewnątrz kąta o mierze: 60^o, znajduje się punkt A odległy od jednego z ramion kąta o 3 od drugiego o 6. Oblicz odległość punktu A do wierzchołka kąta. Rysunek:http://fotowrzut.pl/3QRU1IFLMO W kluczu mam tak: −poprowadzenie przedłużenie odcinka AB i zauważenie miar kątów w trójkątach OBC i DAC −zauważenie, że długość odcinka |AC|=6 oraz ułożenie równania: 6=x√3−6 −> jakiego równania −wyznaczenie x=4√3 −obliczenie odległości |OA|=2√21

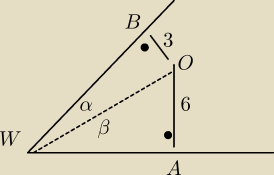
AS: Dane: OA = 6 , OB = 3 , α + β = 60^o , β = 60^o − α

	3		6
OW =		=
	sin(α)		sin(β)

6*sin(α) = 3*sin(60^o − α) Do rozwiązania równanie trygonometryczne 2*sin(α) = sin(60^o − α)