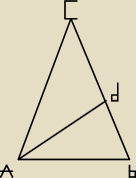
help! Wydi: Punkt D leży na boku BC trójkąta równoramiennego ABC, w którym AC = BC . Odcinek AD dzieli trójkąt ABC na dwa trójkąty równoramienne w taki sposób, że AD = CD oraz AB = BD. Udowodnij, że ∡ADC = 5⋅∡ACD .

Eta: Pomagam

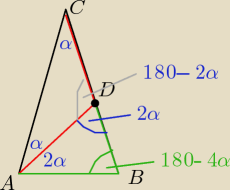
Eta: Teraz już wszystko jasne ΔADC −− równoramienny , to: < CAD = <ACD= α <ADC= 180^o − 2α <ADB= 180^o−(180^o−2α) = 2α ΔABD −−− równoramienny to: <DAB = <ADB= 2α to: < ABD= 180^o − 4α ΔABC −−− równoramienny to: <CAB= <ABC => 3α= 180^o − 4α => 7α= 180^o zatem: <ADC= 180^o −2α= 7α− 2α= 5α i mamy to co chcieliśmy: <ADC= 5*< ACD c.b.d.o Teraz wypiję herbatkę i do Miłych snów Dobranoc Wszystkim "mocnym Markom"

Wydi: Dziękuje

psotka: Witaj Wydi Dopiero dzisiaj ......... podziękowania dla "Ety"?

Wydi: No akurat dziś mogłem powrócić do zadań z maty i od razu chciałem podziękować Trochę czasu minęło wiem ale chyba to nie tragedia psotko