Planime
bezendu:
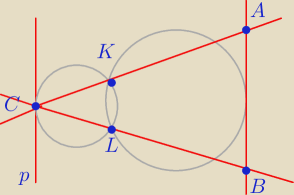
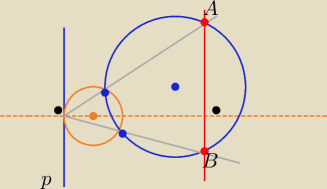
Dwa okręgi przecinają się w punktach K i L. Prosta p jest styczna do pierwszego okręgu w
punkcie C. Proste CK i CL przecinają drugi okrąg odpowiednio w punktach A i B (zobacz
rysunek). Uzasadnij, że prosta p jest równoległa do prostej AB.
Próbowałem coś z talesa ale nie wychodzi
23 kwi 12:10
Wazyl:
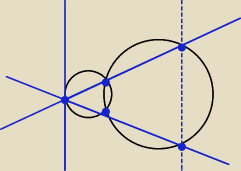
23 kwi 12:20
Domel: Trochę ci się przesunęły punkty A i B
23 kwi 12:20
bezendu:
Trochę tak
23 kwi 12:21
Domel:
1. Jaki uzyskałeś trójkąt
2. Co byś obrał za podstawę trójkąta i jak przebiega wysokość tego trójkąta
3. Jaka jest prosta |AB| do wysokości trójkąta i jaka jest prosta „p” do wysokości
4 No i co z tego wynika
23 kwi 12:25
bezendu:
Trójkąt równoramienny.
Podstawa to AB ?
23 kwi 12:26
Domel:
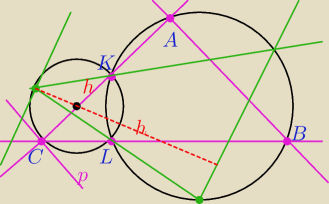
Ale te punkty dotyczą tego konkretnego twojego układu (rysunku) bo np. dla tego mojego rysunku
trzeba by już pomyśleć inaczej.
Np.:
1. Jak biegnie wysokość − zauważ, że wysokość (bez względu gdzie zaznaczysz „C”) będzie
przechodzić przez środek małego okręgu − i co to znaczy
23 kwi 12:43
Domel: Na różowo zrobiłem jeden wariant a na zielono drugi. W różowym wariancie wysokością jest |AC|
23 kwi 12:44
Domel: No a w twoim przypadku pkt 1 i 2
a pkt 3 i 4 to pewnie z rozpędu się zrobi
23 kwi 12:45
bezendu:
Więcej kresek się nie dało ?
prosta p jest prostopadła do wysokości tego trójkąta
mają te same kąty ?
23 kwi 12:48
zawodus: Genialny rysunek
23 kwi 13:33
bezendu:
?
23 kwi 13:37
bezendu: ?
23 kwi 14:00
zawodus: ?
23 kwi 14:05
bezendu: Jak dokończyć ?
23 kwi 14:11
Eta:
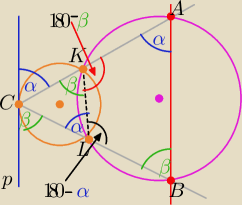
Zaznacz te kąty α i β w trójkącie CLK (z własności kątów dopisanych i wpisanych
Czworokąt AKLB jest wpisany w okrąg ...... z tej własności ....
kąty między siecznymi i prostymi p i AB mają odpowiednio równe miary α, β
to......... p∥ AB
c.n.u
23 kwi 17:34
bezendu:
Dziękuję.
23 kwi 20:19
Eta:
Co tak oschle?
23 kwi 21:25
bezendu:
oschle
?
23 kwi 21:27
Eta:
?
23 kwi 21:29
bezendu:
Chyba na odwrót powinno być.
23 kwi 21:30
bezendu:
A nie da się bez tych kątów dopisanych ?
23 kwi 21:31
Eta:
Da się: p⊥r i AB⊥ r ⇒ p∥ AB
23 kwi 21:33
bezendu:
Ale jak to zrozumieć i to wywnioskować ?
23 kwi 21:34
Eta:
23 kwi 21:38
bezendu:
23 kwi 21:39
Eta:
Co się tak drapiesz?
23 kwi 21:40
bezendu:
Bo jestem de....m i nie nie umiem z planimetrii ?
23 kwi 21:42
Eta:
Jakim "demonem" ?
23 kwi 21:43
bezendu: deb....em
23 kwi 21:43
bezendu:
Eta a co z tego rysunku dalej ?
23 kwi 21:53
Eta:
p⊥ r i AB ⊥ r ⇒
23 kwi 22:00
bezendu:
i zauważenie tego kończy dowód ?
23 kwi 22:02
bezendu:
Dowód na linijkę ?
23 kwi 22:29
bezendu: ?
23 kwi 22:45
Mila:
Bezendu, zostaw te dowody, licz coś.
23 kwi 22:48
bezendu:
Dobrze
23 kwi 23:03
Eta:
23 kwi 23:04