?
Radek:
Bok prostokąta ma długość 24 a przekątna 26. Przekątna dzieli prostokąt na dwa trójkąty. W
każdy z nich wpisujemy okrąg. Oblicz odległość między środkami tych okręgów.
Proszę o rysunek
22 kwi 22:35
zajączek wielkanocny:
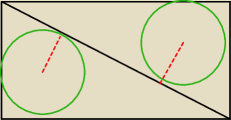
Tak wygląda prostokąt
22 kwi 22:38
Radek:
aleś zabawny aż wcale.... odniosłeś raczej inny efekt
22 kwi 22:39
zajączek wielkanocny:
a tak wygląda prostokąt z przekątną
22 kwi 22:40
zajączek wielkanocny:
a kołeczka sam sobie dorysuj
22 kwi 22:41
Radek:
22 kwi 22:42
jakubs: O zadanko z aksjomatu
22 kwi 22:42
Radek:
Kończ Waść bo nudny jesteś.
22 kwi 22:43
zajączek wielkanocny:
ale przynajmniej wiem jak wygląda prostokąt i nie proszę o rysunek
22 kwi 22:46
Marcin: Ja to zadanie wrzuciłbym sobie do układu współrzędnych, ale to może takie moje zboczenie
22 kwi 22:46
Radek:
Ale żałosny jesteś
22 kwi 22:46
Marcin: Z drugiej strony wiesz, że te dwa okręgi są takie same. Oblicz ich promień.
22 kwi 22:50
22 kwi 22:52
Marcin: ehh. chciałem żeby Radek sam na to wpadł, no ale cóż. Trudno
22 kwi 22:53
Radek:
ale czemu a−2r?
22 kwi 22:55
Wazyl: Cześć wszystkim.
Z tego samego powodu co b−2r.
22 kwi 22:57
Radek:
ale b to wiem ale a nie
22 kwi 22:58
Marcin: Serio? wiesz dlaczego b, a nie wiesz dlaczego a?
22 kwi 22:58
Radek: serio
22 kwi 23:00
Wazyl: Z rysunku:
a=r+r+coś
coś=a−2r
Tak samo z b.
22 kwi 23:00
Marcin:
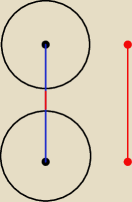
Od czerwonej odejmujesz dwa razy promień okręgu. Czerwona, to długość boku.
22 kwi 23:02
Marcin: u Ciebie w przykładzie jest trochę inaczej, ale idea ta sama
22 kwi 23:03
Radek: ja tam widzę jeden promień
22 kwi 23:03
Marcin: Wyobraź sobie, że te dwa okręgu na siebie najeżdżają.
22 kwi 23:04
Mila:
Radek, narysuj sobie na kartce promienie prostopadłe do podstaw.
22 kwi 23:13
Radek:
Mam rysunek na kartce
22 kwi 23:15
Mila:
Widzisz to, co Ci podpowiadają?
22 kwi 23:25
Radek:
Nie bardzo.
22 kwi 23:28
Radek: ?
22 kwi 23:41
Mila:
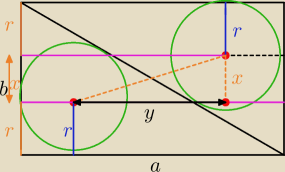
Już Ci to kiedys tłumaczyłam.
x=b−2r
y=a−2r
22 kwi 23:45
Radek:
Ja to zadanie pierwszy raz robię.
i teraz jak ułożyć równanie
(10−2r)2+242=262 ?
22 kwi 23:55
Mila:
Musisz obliczyć r.
x2+y2=|O1O2|2
23 kwi 00:13
Radek:
Ja w tym trójkącie widzę y ale ten mały x (po prawej stronie tego nie rozumiem)
23 kwi 00:18
bezendu:
zobacz tam masz kreski wyraźne, Mila Ci narysowała x=a−2r górny promień i dolny
23 kwi 00:22
Eta:
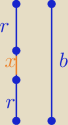
b=r+x+r ⇒ b=2r+x ⇒ x=b−2r
23 kwi 00:27
Radek:
Dziękuję Pani już zrozumiałem
23 kwi 00:30
Eta:
23 kwi 00:34
Radek:
Pomogła by mi Pani jeszcze ?
23 kwi 00:35
Eta:
Pisz zadanie ... za chwilkę będę
23 kwi 00:36
Radek:
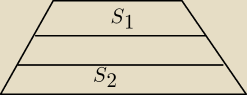
Ramiona trapezu podzielono na trzy równe części prostymi równoległymi do podstaw. Otrzymano w
ten sposób trzy nowe trapezy. Pola skrajnych trapezów wynoszą S
1 i S
2 oblicz pole środkowego
23 kwi 00:42
Radek:
Ale jeszcze to pierwsze coś nie wyjdzie
?
23 kwi 01:11
Marcin: A jaki wyszedł Ci promień?
23 kwi 01:15
Radek:
Jak nie wyszedł właśnie ?
(10−2r)
2+(24−2r)
2=
23 kwi 01:17
Eta:
Hej
Radek
Jak zad. z trapezem? zrobione?
23 kwi 12:19
Radek:
Witam Panią. Nie zrobione, nawet tego pierwszego nie wiem jak dokończyć ?
23 kwi 12:20
Eta:
1/ a=24, b=10, d=26
| | a+b−d | |
to z trójkąta prostokątnego ABD : r= |
| =....... |
| | 2 | |
i |S
1S
2|=y
2+x
2= (a−2r)
2+(b−2r)
2 ⇒ |S
1S
2|=..........
23 kwi 12:29
Radek:
czyli za d podstawić 26 ? 01:17 ?
23 kwi 12:31
Eta:
Dokładnie tak .... i wyznaczysz dł. promienia r=...
23 kwi 12:33
Radek:
ale d to jest przekątna prostokąta a nie ten mały odcinek zaznaczony na rysunku ?
23 kwi 12:36
Radek:
1 już zrobione.
23 kwi 12:40
Eta:
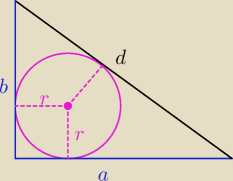
Tak wyznaczamy długość promienia okręgu wpisanego
w trójkąt prostokątny (masz wzór w tablicach)
23 kwi 12:41
Eta:
No...
23 kwi 12:41
Eta:
Będę za 1,5 h ... to Ci napiszę rozwiązanie zad. z trapezem
23 kwi 12:42
Radek:
Dobrze to czekam
23 kwi 12:46
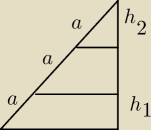
Wazyl: Radek
a) Każdy z nowych trapezów na jakąs wysokość.
Jak ona mają się do siebie?
b) Napisz pola S1 i S2 przy użyciu podstaw.
23 kwi 13:20
23 kwi 13:22
Wazyl: a jak się ma h1 do h3?
23 kwi 13:23
Wazyl: Podpowiem że musisz szukać trójkątów.
23 kwi 13:25
Radek: no nie wiem właśnie ?
23 kwi 13:26
zawodus: Trójkąty podobne
23 kwi 13:29
Wazyl:
23 kwi 13:52
Eta:
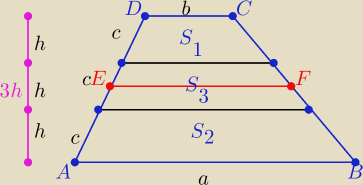
| | a+b | |
Linia środkowa trapezu ABCD = linia środkowa trapezu o polu S3 : |EF|= |
| |
| | 2 | |
| | a+b | | a+b | | 1 | |
S(ABCD)= |
| *3h , S3= |EF|*h = |
| *h ⇒ S3= |
| S ⇒S=3*S3 |
| | 2 | | 2 | | 3 | |
S
3=S−(S
1+S
2) ⇒ ................. dokończ
23 kwi 15:25
Radek:
Ale czemu Pani korzysta z lini środkowej ?
23 kwi 16:51
Eta:
| | a+b | |
No bo tak liczy się pole trapezu .... P(tr)= d*h, d= |
| |
| | 2 | |
23 kwi 17:18
Radek:
| | a+b | |
A to czemu jeszcze S3= |
| *h ? |
| | 2 | |
23 kwi 17:21
Eta:
| | a+b | |
Środkowa |EF| = |
| jest też środkową tego trapezu o polu S3 |
| | 2 | |
zaś jego wysokość to h ( na rys. zobacz)
23 kwi 17:49