planimetria cs: Okręgi o środkach A i B są styczne zewnętrznie i każdy z nich jest jednocześnie styczny do ramion tego samego kąta prostego. Udowodnij, że stosunek promienia mniejszego z tych okręgów do większego jest równa 3−2√2

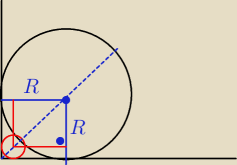
Janek191: r − promień mniejszego okręgu R − promień większego okręgu Mamy ( R − r)² + ( R − r)² = ( R + r)² [ R² − 2R r + r²]*2 = R² + 2 R r + r² 2 R² − 4 R r + 2 r² = R² + 2R r + r² R² − 6 R r + r² = 0 Δ = ( − 6r)² − 4*1*r² = 36 r² − 4 r² = 32 r² = 16²*r² √Δ = 4√2r więc

	6 r − 4√2 r
R =		= 3 r − 2√2 r < r odpada
	2

lub

	6 r + 4√2r
R =		= 3 r + 2√2 r > r
	2

więc

r		r		1
	=		=		= 3 − 2√2
R		3 r + 2√2 r		3 + 2√2

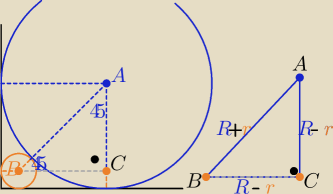ktt: Trójkąt ABC jest prostokątny i równoramienny, to: R+r=(R−r)*√2 ⇒ r+r√2= R√2−R ⇒ r(1+√2)= R(√2−1)

	r		√2−1		(√2−1)2
to		=		=		= 3−2√2
	R		√2+1		2−1

bezendu: Nowe wcielenie Ety

bezendu: Wydał Cię rysunek

Eta: