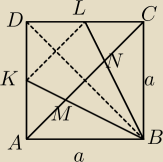
kwadrat Agataku: Dany jest kwadrat ABCD o boku długości a. Punkty K i L są środkami boków kwadratu. Oblicz długość odcinka MN. Moje pytanie jest takie, czy zostałoby uznane gdybym po prostu zauwazyla ze bok wynosi a, wiec przekatna to d=a√2, a MN jest trzecia czescia przekątnej ?

	1		a√2
|MN|=		d=
	3		3

czy bezpieczniej byłoby skorzystac z podobienstwa ? [przerywana linia to dorysowana przeze mnie do rys. ]

fx: To, że zauważyłeś coś jest słabym dowodem bo jak udowodnisz, że w przypadku ogólnym obserwacja na podstawie szczególnego rynku jest prawidłowa? Obserwacja w tym przypadku to zbyt słaby dowód. Raczej skupiłbym się na podobieństwie AMB i BNC.

+-: Z podobieństwa KLB do MNB S i O to punkty przecięcia odcinków KL i MN przez przekątną DB KL/MN=SB/OB

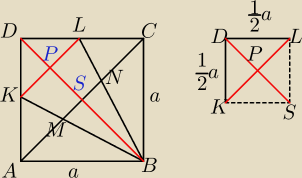Agataku: Zauważenie że jeżeli K i L są środkami boków, to dzielą przekątną na 3 równe części nie byłoby ok? w takim razie KBL i MBN sa podobne

|KL|		|MN|
	=		| * |SB|
|PB|		|SB|

	|KL|
|MN|=		*|SB|
	|PB|

|BD|=2|SB| 2|SB|=a√2 |:2

	a√2
|SB|=
	2

	a√2
|DS|=
	2

	a√2		1
|PS|=		*
	2		2

	a√2
|PS|=
	4

|PB|=|SB|+|PS|

	a√2		a√2
|PB|=		+
	2		4

	3a√2
|PB|=
	4

	1
|KL|=		a*√2
	2

	a√2
|KL|=
	2

	a√2   2		a√2
|MN|=		*
	3a√2   4		2

	2a2
|MN|=
	3a√2

	a√3
|MN|=
	3

Agataku: sorki błąd na końcu oczywiście

	a√2
|MN|=
	3