planimetria
bezendu:
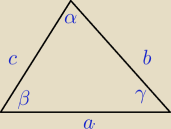
1. Wykaż, że jeżeli kąty wewnętrzne trójkąta spełniają warunek sin α = 2 cos γsin β to trójkąt
ten jest równoramienny
asinβ=bsinα
22 kwi 20:24
Eta:
1 / sposób
z tw. sinusów i tw. cosinusów
| a | | a2+b2−c2 | | 6 | |
| =2* |
| * |
| ⇒ ......... b=c |
| 2R | | 2ab | | 2R | |
22 kwi 20:33
bezendu:
skąd się to wzięło ?
22 kwi 20:35
22 kwi 20:37
zawodus: Do pierwszego równa się twierdzenie sinusów, potem cosinusy
22 kwi 20:37
Eta: 
22 kwi 20:39
bezendu:
Ale czemu 2R a nie tak jak ja wyznaczyłem ?
22 kwi 20:39
Eta:
| | b | |
Poprawiam chochlika w ostatnim ułamku |
| |
| | 2R | |
22 kwi 20:40
Eta:
No i masz gotowca od Mili
22 kwi 20:43
Eta:
Masz tylu chętnych do pomocy
... to ja idę odpocząć
22 kwi 20:46
bezendu:
Nie widzę nigdzie tego gotowca ?
22 kwi 20:50
bezendu: ?
22 kwi 20:52
bezendu:
Odpowie ktoś na moje pytanie ? czemu tam musi być 2R ?
22 kwi 20:57
Saizou : z Tw. sinusów
22 kwi 20:59
bezendu:
Ale nie wychodzi to z tw sinusów wyznaczyłem a i co dalej ?
22 kwi 21:03
Eta:
Mila wykasowała
22 kwi 21:05
bezendu:
No właśnie a biedny maturzysta nadal nie wie !
22 kwi 21:07
bezendu: ?
22 kwi 21:18
Saizou : znowu ktoś wykasował ....
pomyśl o kątach w trójkącie
22 kwi 21:19
Eta:
To była "własność" Mili
22 kwi 21:20
bezendu:
Ale odpowie ktoś na moje pytanie ? 20:39 ?
22 kwi 21:22
bezendu:
22 kwi 21:41
Mila:
1) wykazujesz, że dwa boki równe, sposób Ety
2) albo wykazujesz, że dwa kąty sa równe.
Co chcesz ?
22 kwi 21:45
bezendu:
1.Czemu zostały usunięte dwa posty ?
2. Czemu mam liczyć 2R a nie tak jak zapisałem na początku ?
22 kwi 21:59
Saizou : 2) bo te boku muszą mieć coś wspólnego
22 kwi 22:03
Mila:
Usunęłam swój wpis, bo nie lubisz gotowców, a pisałam zadanie nie patrząc dla kogo, Eta to
zauważyła, więc się "poprawiłam".
2) sinα=2cosγ*sinβ z założenia.
α =180−(γ+β) z sumy katów w Δ.
sinα=sin(180−(γ+β) )=sin(γ+β)
sin(γ+β)=2cosγ*sinβ
teraz rozpisz lewą stronę z wzoru na sinus sumy kątów i dokończ, to jest prosty sposób.
Na pierwsze odpowiem, gdy pomyślę nad Twoim sposobem.
22 kwi 22:24
Mila:
1) to co napisałeś jest dobrze, ale nie prowadzi do celu.
Masz podane założenie:
sinα=2cosγ*sinβ
Z tw. sinusów oblicz sin α, sinβ ( w zależności od odpowiedniego boku i R)
cosγ oblicz z tw. cosinusów i podstaw do wzoru z założenia.
22 kwi 22:34
bezendu:
To skąd mam wiedzieć co wyznaczać w tych zadaniach ? Bo już się w tym zgubiłem....
22 kwi 22:36
Mila:
Patrzysz co masz dane i myślisz jak to wykorzystać, aby udowodnić to , co każą.
21:45 nakreśliłam 2 kierunki. Na pewno są jeszcze inne.
22 kwi 22:52
bezendu:
Dziękuję, choć i tak do matury będę ''ciemny'' z planimetrii
22 kwi 23:30
Mila:
Nie jest tak źle, niektóre zadania rozwiązujesz ładnie.
22 kwi 23:34
Mila:
Dokończyłeś to zadanie dwoma sposobami? Czy napisać.
22 kwi 23:34
bezendu: Nie dokończyłem bo ta planimetria mnie odrzuca.
22 kwi 23:35
Mila:
No to jak będzie?
Rozwiązuj jak, Ci podpowiadałam. Co to za kaprysy?
W matematyce nie ma specjalnej drogi dla królów ( i dla Bezendu).
22 kwi 23:38
bezendu:
Wiem, że nie ma specjalnej drogi, ale nie każdy wszystko rozumie. Z innymi działami nie mam
problemów. A to spróbuje dokończyć
22 kwi 23:39
Mila:
Czekam.
22 kwi 23:48
bezendu:
c
2=a
2+b
2−abcosγ
z tego wychodzi, że b=c
A wracając do tych królików to przydałaby się taka droga
22 kwi 23:53
Mila:
No, no no, tylko nie królików, poczytaj kto to powiedział? I do kogo?
23 kwi 00:08
Mila:
A z kątami?
23 kwi 00:09
bezendu:
a z kątami mam problem.
Wiem już o co chodzi z tymi królikami
23 kwi 00:11
Mila:
(1) sinα=2cosγ*sinβ z założenia.
α =180−(γ+β) z sumy katów w Δ.
sinα=sin(180−(γ+β) )=sin(γ+β)
sin(γ+β)=2cosγ*sinβ
sinγ*cosβ+sinβ*cosγ=2cosγ*sinβ ⇔
sinγcosβ−sinβcosγ=0
sin(γ−β)=0 ⇔
γ=β⇔Δ jest równoramienny.
23 kwi 00:17
Mila:
Dobranoc
23 kwi 00:17
bezendu:
Dziękuję i dobranoc.
23 kwi 00:19