ostroslupy milka: w ostroslupie prawidlowym czworokatnym pole sciany bocznej jest rowne polu podstawy, znajdz sinus kata miedzy przeciwleglymi krawedziami bocznymi tego ostroslupa.

dero2005:

a*hs
	= a2
2

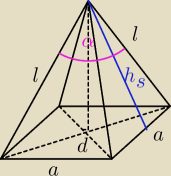
h_s = 2a

	a
l = √hs2 + (a2)2 =		√17
	2

d = a√2 d² = 2l² − 2l²cosα −−−−−−−−−−−−−−−−−−−−−−−− _____−−−−−−−−−−____

	13
cosα =
	17

	2
sinα = √1 − cos2α =		√30
	17

milka: troszeczke nie rozumiem tego d² = 2l² − 2l²cosα

dero2005: wzór cosinusów

milka: kurcze... czy wszystkie zadania trzeba robic z twierdzen sinusow i cosinusow? nie mamy tego na podstawie i troszeczke ciezko ogarnac: D

milka: jest jakis inny sposob?

dero2005: h_s = 2a

	a
l = √hs2 + (a2)2 =		√17
	2

d= a√2

d   2		√34
	= sinα2 =
l		17

ze wzoru

	1−cosα
sinα2 = √
	2

	13
cosα = 1 − 2*sin2α2 =
	17

	2
sinα = √1 − cos2α =		√30
	17

taki sposób pasuje?