Trygonometria
Qmi:
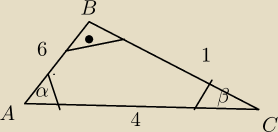
W trójkącie prostokątnym ABC (kąt prosty przy wierzchołku B)
| | 1 | |
Sinus kąta ACB jest równy |
| i |AB| = 6. Oblicz obwód tego trójkąta |
| | 4 | |
Obwód = 11?
| | 1 | |
Nie ogarniam: ,,Sinus kąta ACB jest równy |
| i |AB| = 6." |
| | 4 | |
Przy którym rogu powinienem postawić ten kąt. w sumie nie może leżeć tam gdzie leży β no bo na
przeciwko jest 6.
22 kwi 14:40
Qmi: ~ podbijam
22 kwi 14:50
Marcin:
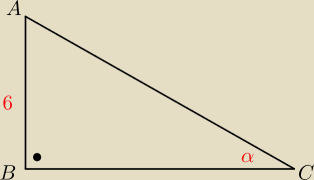
22 kwi 14:53
Qmi: i α jest zawsze tam gdzie jest środkowa litera? Czyli w tym przypadku pod C.
A gdyby było ABC to byłaby tam gdzie jest B ?
22 kwi 14:54
razor: taki trójkąt który narysowałeś nie istnieje

4+1 < 6 z nierówności trojkąta. U ciebie sinus
| | 6 | | 1 | |
kąta ACB jest równy |
| , a ma być równy |
| − ile musi wynosić w takim razie |AC|? |
| | 4 | | 4 | |
22 kwi 14:55
katB: Załóżmy :
|AB| = a
|BC| = b
|AC| = c
sinβ = 1/4
|AB| = 6
sinβ = a/c
1/4 = 6/c
c = 24
Sam nie wiem czy dobrze myślę. Ale staram się rozwiązać zadanie , bo mnie zaciekawiło.
22 kwi 14:55
Marcin: 24=x
Przeciwprostokątna ma 24.
22 kwi 15:00
katB: a z jedynki trygonometrycznej
sin
2x + cos
2x = 1
Jak się obliczy cosinusa to można |BC| obliczyć z cosβ = b/c



22 kwi 15:02
Marcin: Można, tylko nie wiem po co tak kombinować

22 kwi 15:04
Marcin: Qmi tak jak napisałeś

α jest zawsze tam, gdzie 'środkowa litera'
22 kwi 15:04
katB: równanie pitagorasa zastosuj, będzie łatwiej :
a2 + b2 = c2
62 + b2 = 242
b2 = 576 − 36
b2 = 540
b = √540
b = √36*15
b = 6√15
Obwód = 6√15 + 6 + 24 = 30 + 6√15
22 kwi 15:07
Qmi: Dzięki wszystkim

22 kwi 15:10
katB: 
22 kwi 15:10
 W trójkącie prostokątnym ABC (kąt prosty przy wierzchołku B)
W trójkącie prostokątnym ABC (kąt prosty przy wierzchołku B)

 4+1 < 6 z nierówności trojkąta. U ciebie sinus
4+1 < 6 z nierówności trojkąta. U ciebie sinus




 α jest zawsze tam, gdzie 'środkowa litera'
α jest zawsze tam, gdzie 'środkowa litera'

