funkcja wymierna, zbiór wartości alik: Wyznacz zbiór wartości funkcji f(x)=(x−1)²/x²+1 chciałam rozpocząć od wykresu, ale nawet nie wiem jak go narysować, będę wdzięczna za pomoc!

Hajtowy:

	(x−1)2
f(x)=
	x2+1

D_f = R x₀ = 1 Podstaw sobie liczby za 'x' i rysuj

ICSP: Masz wyznaczyć zbiór wartości a nie rysować wykres.

bezendu: To ja sposobem z zbioru A.Kiełbasy

	(x−1)2
f(x)=
	x2+1

x2−2x+1
	=p
x2+1

x²−2x+1=x²p+p x²−x²p−2x+1−p=0 I należy rozpatrzeć dwa przypadki

pigor: ..., np. tak : w zbiorze D=R niech

	(x−1)2
f(x)=w ⇔ w=		⇔ wx2+w= x2−2x+1 ⇔ (w−1)x2+2x+w−1=0
	x2+1

i równanie to ma rozwiązanie ⇔ Δ_m ≥0 ⇔ 4−4(m−1)² ≥0 ⇔ 1−(m−1)² ≥0 ⇔ ⇔ (w−1)²≤ 1 ⇔ |w−1|≤ 1 ⇔ −1≤ w−1≤ 1 /+1 ⇔ 0≤ w≤ 2 ⇔ w∊<0;2> − − szukany zbiór wartości w danej funkcji f. ...

bezendu: I pigor dokończył moją myśl

Maslanek: Zauważmy, że

	(x−1)2		x2+1−2x		2x
f(x)=		=		=1−
	x2+1		x2+1		x2+1

	x
Rozpatrzmy funkcję: h(x)=
	x2+1

Zbadajmy jej monotoniczność: Niech x, y∊R takie, że y−x>0

	x		y		xy2+x−yx2−y
Wtedy h(x)−h(y)=		−		=		=
	x2+1		y2+1		(y2+1)(x2+1)

xy(y−x)+(x−y)		(y−x)(xy−1)
	=
(y2+1)(x2+1)		(y2+1)(x2+1)

y−x>0 z założenia W zależności od znaku (xy−1) mamy funkcję rosnącą lub malejącą. Co wtedy będzie się działo?

Maslanek: Ładny sposób Już zapomniałem jak to się robi w prosty sposób

ZKS:

(x − 1)2		x2 + 1 − 2x		2x
	=		= 1 −
x2 + 1		x2 + 1		x2 + 1

−(x − 1)² ≤ 0 ≤ (x + 1)² −(x² + 1) + 2x ≤ 0 ≤ x² + 1 + 2x

	1
−(x2 + 1) ≤ −2x ≤ x2 + 1 / *
	x2 + 1

	2x
−1 ≤ −		≤ 1
	x2 + 1

	2x
0 ≤ −		+ 1 ≤ 2 ⇒ ZWf = [0 ; 2].
	x2 + 1

ICSP: Inny sposób : −(x−1)² ≤ 0 ≤ (x + 1)² −x² + 2x − 1 ≤ 0 ≤ x² +2x + 1 // − 2x −(x² + 1) ≤ −2x ≤ (x² + 1) // : (x² + 1) > 0

	2x
−1 ≤ −		≤ 1 // + 1
	x2 + 1

	(x − 1)2
0 ≤		≤ 2
	x2 + 1

f(R) = [0 ; 2]

alik: DZIEKUJE BARDZO, JUZ ROZUMIEM! JESTEŚCIE SUPER!

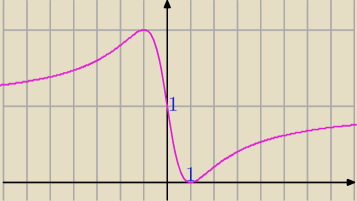
Domel: A tu potwierdzenie graficzne