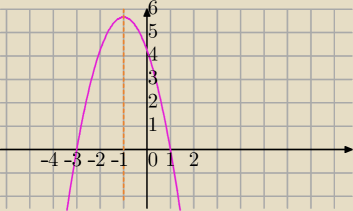
Obliczanie delty-pierwiastek Bardock: Witam! Proszę o pomoc w obliczeniu delty, ponieważ natrafiłem na problem podczas przekształcania postaci ogólnej funkcji kwadratowej na postać kanoniczną. P− wyszło mi dobrze, ale q nie bardzo i przypuszczam, że problem tkwi poniżej: Δ= (−2√2)² − 4* (−√2)* 3√2 Moje obliczenia dały mi wynik: 20√4 Wzór ogólny funkcji: f(x)= −√2 * (x+3) * (x−1) Z góry dziękuję za pomoc.

ZKZ: Podales wzor w postaci iloczynowej a nie ogolnej

zajączek wielkanocny: (−2√2)² = 8, −4*(−√2)*3√2 = 12, 8 + 12 = 20

Mila: Nie musisz liczyć delty, gdy masz postać iloczynową.

	x1+x2		−3+1
xw=		=		=−1 (oś symetrii paraboli)
	2		2

y_w=−√2*(−1+3)*(−1−1)=−√2*(−4)=4√2 postać kanoniczna: f(x)=−√2*(x+1)²+4√2

Bardock: Dziękuję za odpowiedzi, czyli w postaci iloczynowej mogłem od razu wykorzystać miejsca zerowe. Zastanawiałem się nad tym, ale pewien nie byłem. Dziękuję Mila. Zajączku wielkanocny, a możesz mi powiedzieć jak Ci wyszło: −4*(−√2)*3√2 = 12? Gdzieś popełniam błąd, w takim razie: 4√2* 3√2 =12√4= 12*2= 24? Dziękuję za odpowiedź.

Bardock: Może mi ktoś wytłumaczyć dlaczego wyszło 12 lub rozpisać to bardziej "łopatologicznie"? −4*(−√2)*3√2 = 12 Przeszukałem działania na pierwiastkach i próbowałem na różne sposoby, ale bezskutecznie.