kąt między sąsiednimi krawędziami bocznymi niz: Stosunek powierzchni bocznej do powierzchni podstawy ostrosłupa prawidłowego czworokątnego jest równy k. b)Wyznacz cosinus kąta zawartego między sąsiednimi krawędziami bocznymi tego ostrosłupa. Oblicz miarę tego kąta dla k=√3. c) Wykaż, że cosα=−1/k2, gdzie α jest kątem między sąsiednimi ścianami bocznymi tego ostrosłupa. odp b: cosα=(k²−1)/(k²+1) , α=60

dero2005:

Pb
	= k = √3
Pp

2a*hs
	= √3
a2

	a
hs =		√3
	2

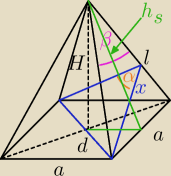
l² = h_s² + (^a₂)² l = a a² = 2l² − 2l²cosβ a² = 2a² − 2a²cosβ

	1
cosβ =
	2

β = 60^o ____________________ x*l = a*h_s

	a*hs		a
x =		=		√3
	l		2

d = a√2 d² = 2x² − 2x²cosα 2a² = 2(^a√3₂)² − 2(^a√3₂)²cosα

	1		1		1
cosα = −		= −		= −
	3		(√3)2		k2