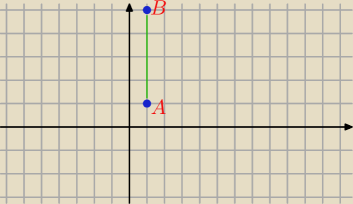
123 Mycha: dane sa punkty a(1, 1) i b(1,5) znajdz taki punkt c na osi y aby trojkat abc byl trojkatem prostokatnym o kacie prostym przy wierzcholku c

fx: Rysunek zrób.

5-latek:

Mycha: wiem jak to ma wygladac ale nie wiem jak wyznaczyc punkt

ICSP: a punkt C jakie będzie miał współrzędne? Czy znasz którą z nich? Czy potrafisz policzyć długości odcinków AC , BC , AB ? Znasz jakieś twierdzenie dotyczące trójkąta prostokątnego wykorzystujące długości jego boków ?

Mycha: punkt C (0, y)

ICSP: a ja oznaczę C( 0 , y_c) aby było wiadomo czym jest ten y Teraz długości boków AC , BC , AB poproszę

Dziadek Mróz: |AC|² + |BC|² = |AB|² |AB| = √(x_B − x_A)² + (y_B − y_A)²

Mycha: wlasnie robie i wyszlo mi takie cos: √(0−1)²+(yc−1)² + √(0−1)²+(yc−5)²

Mycha: i potem wychodzi rownanie kwadratowe

ICSP: |AC| = ? |BC| = ? |AB| = ?

zombi: Swoją drogą, z wektorów chyba szybciej idzie. Mamy wektory AC^→ = [1; 1−y_c] BC^→ = [1; 5−y_c] Jeśli AC^→ ◯ BC^→ = 0 to wektory AC i BC są prostopadłe, więc mamy 1*1 + (1−y_c)(5−y_c) = 0 I wyznaczymy y_c, dla których będą prostopadłe. To się chyba nazywa fachowo ortogonalność.

Mycha: wektorow to ja na podstawie nie ogarniam.: ) nie wiem jak wyciagnac pierwiastek z tych rownan kwadratowych..

fx: Korzystasz z własności: √x² = |x|

Mycha: ale mam tak: √yc²−2yc+2 + √yc²−10yc+26 = 16 i nie wiem.......

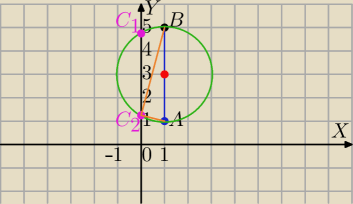
Mila: środek AB: S=(1,3) rysujesz okrąg ośrodku S i promieniu 2. AB jest średnicą okręgu ∡AC₂B jest kątem wpisanym w okrąg opartym na średnicy, zatem jest prosty. ∡AC₁B jest kątem wpisanym w okrąg opartym na średnicy, zatem jest prosty. (x−1)²+(y−3)²=4 x=0 (0−1)²+(y−3)²=4 (y−3)²=3 y−3=√3 lub y−3=−√3 y=3+√3 y=3−√3 C₁=(0,3+√3 C₂=(0,3−√3)