Dany jest trójkąt ABC, w którym |AC| = 17 i |BC| = 10. Na boku AB leży punkt D t kamczatka: Dany jest trójkąt ABC, w którym |AC| = 17 i |BC| = 10. Na boku AB leży punkt D taki, że |AD| : |DB| = 3 : 4 oraz |DC| = 10. Oblicz pole trójkąta ABC. Czemu mi to nie wychodzi za pomocą twierdzenia cosinusów ? liczę tak: 17² = 49x² + 100 − 140cosα 289 = 49x² + 100 − 140xcosα 0= 49x² − 189 − 140xcosα robię gdzieś błąd czy się nie da za pomocą twierdzenia cosinusów obliczyć tego ?

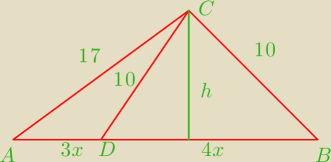
bezendu: h²=10²−(2x)² h²=17²−(5x)²

kamczatka: tak wiem tym sposobem można, ale czy z twierdzenia cosinusów się nie da?

kamczatka: ?

bezendu: i co Ci te cosinusy tu dadzą ?

kamczatka: jakbym miał wartość cosβ przy wierzchołku B to potem bym mógł obliczyć x'a

bezendu: Ja to widzę tylko z pitagorasa. A po dwa tam masz x więc raczej nie.