456
007: Wysokość trójkąta równoramiennego ABC opuszczona z wierzchołka C na podstawę AB ma długość 2, a
kąt przy wierzchołku C ma 120stopni. Proste zawierające wysokość tego trójkąta przecinają się
w pukncie S. Znajdź wysokość trójkąta ABS opuszczonąz wierzchołka S.
odp to 6, a jakim cudem to moze byc dluzsze od wysokosci trojkata?

21 kwi 10:02
5-latek:

CD=2
teraz kombinuj
21 kwi 10:28
Ted:
... wysokości lub ich przedłużenia przecinają się w jednym punkcie ... i wcale nie musi on
leżeć wewnątrz trójkąta −

... te rysunek trochę łudzi −

21 kwi 10:42
5-latek: A jaki bys narysowal do tego zadania

21 kwi 10:57
5-latek: Poza tym autora nie ma na forum wiec nie bede sie produkowal

21 kwi 11:00
Ted:
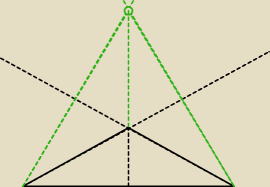
21 kwi 11:04
5-latek: Tak taki moze byc jesli sie narysuje dokladny rysunek za pomoca linijki i kątomierza
Wtedy ladnie widac

21 kwi 11:36
007: o, wiec jednak dobrze, dzieki

21 kwi 11:43
5-latek: Ale grunt to zrobic rysunek . Nie ?
21 kwi 11:45
Bogdan:
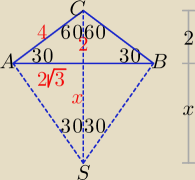
x = 2
√3*
√3 = ...
Dobry i rzetelny rysunek to gwarancja sukcesu, nie można tego elementu zadania traktować
po macoszemu, rysunek ma wspomóc rozumienie i rozwiązanie zadania, nie może być mylący
i nie może przeszkadzać.
21 kwi 11:53
Ted:
... tyle Bogdanie, że Twój punkt S nie ma nic wspólnego z wysokościami opuszczanymi
z A i B
21 kwi 15:11
Ted:
... przynajmniej nie pokazujesz tego na rysunku −

21 kwi 15:12
Eta:
Na rysunku jest:
|∡SAC|=|∡SBC|=90o ( jasne?
21 kwi 15:22
Bogdan:
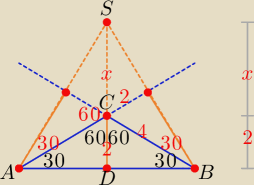
Wysokość trójkąta wychodząca z wierzchołka zawiera się w prostej prostopadłej
do prostej zawierającej bok trójkąta, proste zawierające wysokości trójkąta przecinają się
w jednym punkcie.
W tym zadaniu nie miało znaczenia, w którym kierunku zostaną poprowadzone proste
zawierające wysokości trójkąta.
Na tym rysunku x = 4 i |SD| = 6
21 kwi 16:13
Ted:
sądziłem, że matematyka to nauka ścisła.
Ale po bzdurach wypisywanych przez Eta zwątpiłem.
21 kwi 18:35
Eta:
Ted jesteś "świątecznie miły"

pozdrawiam
21 kwi 19:00
Ted:
... twój post Eta z 15:22 był bardzo ale to bardzo przemiły.
21 kwi 21:10

 CD=2
teraz kombinuj
CD=2
teraz kombinuj
 ... te rysunek trochę łudzi −
... te rysunek trochę łudzi −





 x = 2√3*√3 = ...
Dobry i rzetelny rysunek to gwarancja sukcesu, nie można tego elementu zadania traktować
po macoszemu, rysunek ma wspomóc rozumienie i rozwiązanie zadania, nie może być mylący
i nie może przeszkadzać.
x = 2√3*√3 = ...
Dobry i rzetelny rysunek to gwarancja sukcesu, nie można tego elementu zadania traktować
po macoszemu, rysunek ma wspomóc rozumienie i rozwiązanie zadania, nie może być mylący
i nie może przeszkadzać.

 Wysokość trójkąta wychodząca z wierzchołka zawiera się w prostej prostopadłej
do prostej zawierającej bok trójkąta, proste zawierające wysokości trójkąta przecinają się
w jednym punkcie.
W tym zadaniu nie miało znaczenia, w którym kierunku zostaną poprowadzone proste
zawierające wysokości trójkąta.
Na tym rysunku x = 4 i |SD| = 6
Wysokość trójkąta wychodząca z wierzchołka zawiera się w prostej prostopadłej
do prostej zawierającej bok trójkąta, proste zawierające wysokości trójkąta przecinają się
w jednym punkcie.
W tym zadaniu nie miało znaczenia, w którym kierunku zostaną poprowadzone proste
zawierające wysokości trójkąta.
Na tym rysunku x = 4 i |SD| = 6
 pozdrawiam
pozdrawiam