trygonometria
lala: Bardzo proszę o pomoc, nie wiem co z tym zrobić....próbowałam coś wyciągnąć przed nawias żeby
skrócić do wzoru ale nic mi nie idzie.
Wykaż, że dla każdej liczby x∈ R prawdziwa jest nierówność
|3 sin x +2 cos x | ≤ 13
20 kwi 16:28
lala: 2. Wyznacz wszystkie wartości parametru a ∈ <0; 2 π>,dla których równanie
(2x sina — y — 1)2 + (x — 2y sina — 1 )4 = O nie ma rozwiązań.
20 kwi 16:42
lala: 3. Rozwiąż równanie cos x/2 + cos x/3 = 2.
20 kwi 16:44
lala: pomoże ktoś? chociaż jakas wskazówka?
20 kwi 21:16
Utem:
1) |a+b|≤|a|+|b| i ograniczenie sinx , cosx
2)Łatwiej wyznaczyć α dla których równanie ma rozwiązanie,
2x sina− y −1=0
x −2y sina −1 =0 metoda wyznaczników
| | x | | x | |
3) cos |
| =1 i cos |
| =1 jednocześnie maja być równe1. |
| | 2 | | 3 | |
20 kwi 22:06
Utem:
3) x=12kπ
20 kwi 22:13
Mila:
20 kwi 22:14
lala:
1. niestety dalej nie wiem co z tym zrobić, może ktoś wytłumaczyć?
2. jasne
3. wychodzi x=4π i x=6π, czyli odpowiedzią jest nww tak?
dziękuje za pomoc utem

21 kwi 15:41
razor: Jesteś pewna że w 1. po prawej stronie jest 13 a nie √13? Jeśli 13 to banalne
21 kwi 15:44
lala: √13, przepraszam,źle przepisałam
21 kwi 16:08
Beforeu: w 1szym
|3sinx+2cosx| ≤ √13
√(3sinx+2cosx)2 ≤ √13
(3sinx+2cosx)2 ≤13 no i dalej to juz dasz rade
21 kwi 16:36
lala: hmm rozpisałam ze wzoru i zamieniłam z jedynki trygonometrycznej i wyszło 5 sin2+12sinxcosx−9
≤0 ale nie wiem jak to zamienić żeby wyszedł sam sinus albo cosinus
21 kwi 16:53
21 kwi 16:57
Beforeu: ze wzoru na sinusa podwojnego kata 12sinx cosx = 6 sin2x
21 kwi 17:59
lala: no można, ale to mi nic chyba nie da, bo równania 5sin2x+6sin2x−9≤0 przecież też nie rozwiąże
21 kwi 18:13
pigor: ..., wykaż, że dla każdej liczby x∈R prawdziwa
jest nierówność
|3sinx+2cosx| ≤√13.
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
..., no to może np. tak: mianowicie zauważ,
że
|3sinx+2cosx|2= (3sinx+2cosx)
2 ≤ (3sinx+2cosx)
2 +(2sinx−3cosx)
2=
= 9sin
2x+12sinxcosx+4cos
2x +4sin
2x−12sinxcosx+9cos
2x= 13(sin
2x+cos
2x)=
13
zatem
3sinx+2cosx| ≤ √13 . c.n.w. . ...

21 kwi 18:48
Beforeu: a co jesli 3sinx+2cosx jest ujemne

?
21 kwi 18:56
pigor: ... , nic, bo nad tym "czuwa" (dba o to) wartość bezwzględna
(":zjadłem" ją od lewej strony w ostatniej linijce − przepraszam) . ...

21 kwi 19:07
lala: faktycznie,już rozumiem dziękuje wszystkim, w życiu bym na to nie wpadła.
Mam jeszcze jedno, jakby ktoś mógł pomóc:
Wyznacz liczbę rozwiązań równania x3−3x2−9x=m w przedziale <−2,4> w zaleznosci od parametru m
pierwiastki to 0, 3−3√52 i 3+3√52 i co moge z tym zrobić?
21 kwi 19:43
lala: wie ktoś?
21 kwi 22:15
.:
Możesz narysować przybliżony wykres funkcji i na jego podstawie w przedziale <−2, 4> ocenić
ilość rozwiązań.
21 kwi 22:20
Mila:
Pochodne znasz?
21 kwi 22:20
razor: jaki poziom? pytanie czy wiesz jak badać przebieg zmienności funkcji
21 kwi 22:22
razor:
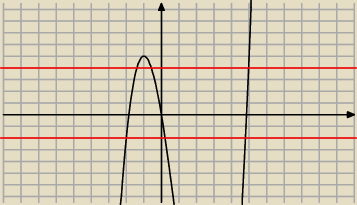
21 kwi 22:23
21 kwi 22:27
lala: matura, ani pochodnych ani przebiegu zmienności funkcji.
tylko że żeby narysować wykres funkcji i dobrze odczytać potrzebuje wierzchołki a ich nie umiem
wyznaczyć, da się jakoś je obliczyć bez pochodnych?
21 kwi 22:34
Mila:
Lala, to zadanie pewnie z matur, gdy badano przebieg funkcji.
21 kwi 22:42
lala: możliwe, bo to 2007, czyli nie da się tego rozwiązać innym sposobem?
21 kwi 22:44
Mila:
Poszukaj klucza, to się przekonasz. Na razie zostaw to zadanie.
21 kwi 22:46
lala: w sumie to nawet nie jest z matury cke, tylko z jakiejś gazety, więc nie mogę nawet sprawdzić.
Może się rzeczywiście na moim poziomie nie da, chyba że coś komuś wpadnie to piszcie. Dziękuję

21 kwi 22:49


 ?
?


