19 kwi 22:56
Tadeusz:
... a czegóż tam nie rozumiesz? −
19 kwi 23:10
$: nie za bardzo mogę wyobrazić sobie tą odległość d
Da się to narysować to co mi potrzebne na płasko ?
19 kwi 23:12
Utem:
Zacieniuj podstawę − ΔABC, to ujrzysz to w przestrzeni.
19 kwi 23:14
Tadeusz:
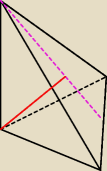
19 kwi 23:17
$: no już jakoś to powiedzmy widzę, i jak z tym dalej ruszyć
jakieś pole na 2 sposoby tak ?
19 kwi 23:35
Tadeusz:
... to może przeczytaj treść zadania
Policzyć masz objętość.
Daną masz długość boku podstawy i odległość wierzchołka od przeciwległej ściany.
Do policzenia objętości potrzebujesz wysokość ostrosłupa
19 kwi 23:58
$:
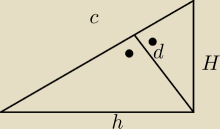
mam taki rysunek
h i d są podane
mam wyliczyć H
h*H=c*d
tylko nie wiem jak c uzależnic od h i d
cos porobilem i wyszło ze
c=(h
2−d
2)+(H
2−d
2)
ale pewnie źle
20 kwi 00:09
pigor: ..., masz układ równań z tw. Pitagorasa i porównania
wzorów na pole Δ np. taki :
c
2=h
2+H
2 i Hh=cd /
2 ⇔ c
2=h
2+H
2 i H
2h
2= (h
2+H
2)d
2 ⇒
| | hd | |
⇒ H2(h2−d2)= h2d2 ⇒ H= |
| . ... |
| | √h2−d2 | |
20 kwi 00:34
Bogdan:
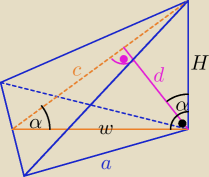
| | 1 | |
w = |
| a√3, c = √w2 + H2 |
| | 2 | |
Pole przekroju będącego trójkątem prostokątnym o przyprostokątnych w, H i przeciwprostokątnej c
| | 1 | | 1 | |
P = |
| cd = |
| wH, stąd można wyznaczyć H |
| | 2 | | 2 | |
20 kwi 00:58