a
123: jak to narysować
f(x)= ||2x−1|−2| −1
19 kwi 15:29
Tadeusz:
rysujesz:
f(x)=2x−1
f(x)=|2x−1|
f(x)=|2x−1|−2
f(x)=||2x−1|−2|
f(x)=||2x−1|−2|−1
19 kwi 15:34
123: to 2x−1 to 2x i w prawo przesunięty ?
a ta reszta −2 i ostatnie −1 to w dół ?
miałem podac miejsca zerowe i zbiór wartośći
wyszło mi jakoś tak
y∊ <−1, +∞)
mz: −1, 0 , 1, 2
19 kwi 15:38
Tadeusz:
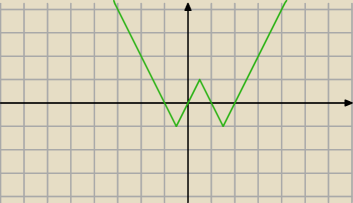
19 kwi 16:30
Domel:
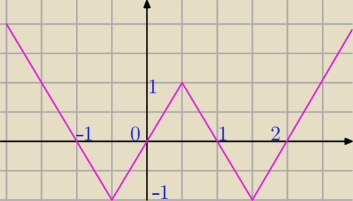
f(x)= ||2x−1|−2| −1
dla |2x − 1|
x∊(−oo; 0,5) => |2x − 1| = −2x + 1 x∊<0,5; +oo) => |2x − 1| = 2x − 1
|−2x + 1 −2| = |−2x −1| |2x − 1 − 2| = |2x − 3|
x∊(−oo; −0,5> => |−2x −1| = −2x − 1 x∊<0,5; 1,5) => |2x − 3| = −2x + 3
−2x − 1 − 1 = −2x − 2 −2x + 3 − 1 = −2x + 2
x∊(−0,5; 0,5) => |−2x −1| = 2x + 1 x∊<1,5; +oo) => |2x − 3| = 2x − 3
2x + 1 − 1 = 2x 2x − 3 − 1 = 2x − 4
x∊(−oo; −0,5> => f(x) = −2x − 2
x∊(−0,5; 0,5) => f(x) = 2x
x∊<0,5; 1,5) => f(x) = −2x + 2
x∊<1,5; +oo) => f(x) = 2x − 4
To by było chyba tak

19 kwi 17:02

 f(x)= ||2x−1|−2| −1
dla |2x − 1|
x∊(−oo; 0,5) => |2x − 1| = −2x + 1 x∊<0,5; +oo) => |2x − 1| = 2x − 1
|−2x + 1 −2| = |−2x −1| |2x − 1 − 2| = |2x − 3|
x∊(−oo; −0,5> => |−2x −1| = −2x − 1 x∊<0,5; 1,5) => |2x − 3| = −2x + 3
−2x − 1 − 1 = −2x − 2 −2x + 3 − 1 = −2x + 2
x∊(−0,5; 0,5) => |−2x −1| = 2x + 1 x∊<1,5; +oo) => |2x − 3| = 2x − 3
2x + 1 − 1 = 2x 2x − 3 − 1 = 2x − 4
x∊(−oo; −0,5> => f(x) = −2x − 2
x∊(−0,5; 0,5) => f(x) = 2x
x∊<0,5; 1,5) => f(x) = −2x + 2
x∊<1,5; +oo) => f(x) = 2x − 4
To by było chyba tak
f(x)= ||2x−1|−2| −1
dla |2x − 1|
x∊(−oo; 0,5) => |2x − 1| = −2x + 1 x∊<0,5; +oo) => |2x − 1| = 2x − 1
|−2x + 1 −2| = |−2x −1| |2x − 1 − 2| = |2x − 3|
x∊(−oo; −0,5> => |−2x −1| = −2x − 1 x∊<0,5; 1,5) => |2x − 3| = −2x + 3
−2x − 1 − 1 = −2x − 2 −2x + 3 − 1 = −2x + 2
x∊(−0,5; 0,5) => |−2x −1| = 2x + 1 x∊<1,5; +oo) => |2x − 3| = 2x − 3
2x + 1 − 1 = 2x 2x − 3 − 1 = 2x − 4
x∊(−oo; −0,5> => f(x) = −2x − 2
x∊(−0,5; 0,5) => f(x) = 2x
x∊<0,5; 1,5) => f(x) = −2x + 2
x∊<1,5; +oo) => f(x) = 2x − 4
To by było chyba tak 