x
Mario: Pole trojkata o wierzcholkach A(1;−2)i B(2;3) jest rowne 8.
Obliczyc wspolrzedne trzeciego wierzcholka,wiedzac,ze nalezy do prostej 2x−y−2=0
|AB|=
√26
Przyda mi sie to?Co dalej?
19 kwi 13:30
Radek:
Masz wzór w tablicach za pomocą wyznaczników
C=(x,2x−1)
19 kwi 13:34
J: H = odległość szukanego punktu C od prostej AB oraz C należy do prostej ... układ równań
19 kwi 13:34
BoosterXS: Masz prostą w postaci ogólnej, sprowadź do postaci kanonicznej i ładnie narysuj w układzie
współrzędnych, pozaznaczaj znane wierzchołki. Wierzchołek nieznany(C) będzie miał współrzędne
(x,2x−2).
19 kwi 13:35
Bogdan:
Propozycja rozwiązania: A(1, −2), B(2, 3), C(x
c, y
c) = (x
c, 2x
c − 2)
Pomijam znak strzałki nad zapisem wektora
CA = [1 − x
c, −2 − (2x
c − 2)], CB = [2 − x
c, 3 − (2x
c − 2)]
|1−x
c −2x
c|
8 = 0,5*| | |
|2−x
c 5−2x
c|
16 = |(1 − x
c)(5 − 2x
c) − (−2x
c)(2 − c
c)|
trzeba rozwiązać to równanie z wartością bezwzględną
19 kwi 13:43
Mario: AB ∊ do prostej m:5x−y−7=0
Znachodze x z odl. punktu (x,2x−2) do prostej m
moze tak wyjsc?
19 kwi 13:47
Mario: zaraz sprawdze,akurat chcialem zapytac o ktorych tablicach Radek mowil)juz kojarze
dziekuje
19 kwi 13:49
Mario: | | 2 | |
przez wyznaczniki x = 3 |
| lub x = 7 |
| | 11 | |
19 kwi 13:54
5-latek:
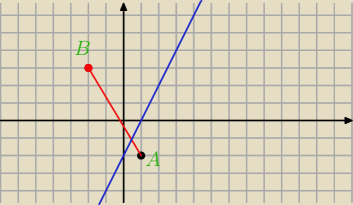
Z tego rysunku widac ze beda takie dwa punkty
19 kwi 13:58
5-latek: Skopalem rysunek

19 kwi 14:00
 Propozycja rozwiązania: A(1, −2), B(2, 3), C(xc, yc) = (xc, 2xc − 2)
Pomijam znak strzałki nad zapisem wektora
CA = [1 − xc, −2 − (2xc − 2)], CB = [2 − xc, 3 − (2xc − 2)]
|1−xc −2xc|
8 = 0,5*| | |
|2−xc 5−2xc|
16 = |(1 − xc)(5 − 2xc) − (−2xc)(2 − cc)|
trzeba rozwiązać to równanie z wartością bezwzględną
Propozycja rozwiązania: A(1, −2), B(2, 3), C(xc, yc) = (xc, 2xc − 2)
Pomijam znak strzałki nad zapisem wektora
CA = [1 − xc, −2 − (2xc − 2)], CB = [2 − xc, 3 − (2xc − 2)]
|1−xc −2xc|
8 = 0,5*| | |
|2−xc 5−2xc|
16 = |(1 − xc)(5 − 2xc) − (−2xc)(2 − cc)|
trzeba rozwiązać to równanie z wartością bezwzględną
 Z tego rysunku widac ze beda takie dwa punkty
Z tego rysunku widac ze beda takie dwa punkty
