Dla jakiego parametru m równanie x^2 -(m + 2)x + m + 5 = 0 ma dwa różne pierwias kamczatka: Dla jakiego parametru m równanie x² −(m + 2)x + m + 5 = 0 ma dwa różne pierwiastki spełniające warunek x₁² + x₂² ≤ −3m 1. Δ > 0 [−(m+2)²] − 4(m + 5) > 0 m² +4m +4 − 4m − 20 > 0 m² − 16 > 0 (m −4)(m + 4) > 0 m∊ (−∞;−4) ∪ (4;∞) 2. 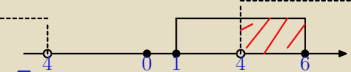x₁² + x₂² ≤ −3m (x₁ + x₂)² −2x₁x₂ (m + 2)² −2(m + 5) ≤ −3m m² +4m +4 −2m −10 ≤ −3m m² +4m +4 −2m −10 +3m ≤ 0 m² +5m −6 ≤ 0 m₁ = 6 m₂ = 1 x∊ <1;6> i mi część wspólna obu przedziałów wychodzi taka: x∊(4;6> dobrze ?

5-latek:

kamczatka: czyli chyba dobrze ? bo w odpowiedziach mam wynik : <−6;−4)

ICSP: m² + 5m − 6 ≤ 0 m² + 6m − m − 6 ≤ 0 (m+6)(m−1) ≤ 0 m ∊ [−6 ; 1] Przypadki 1^o i 2^o łączymy spójnikiem koniunkcji i dostajemy odp x ∊ [−6 ; 4)

5-latek: ja rysowalem z Toich obliczen Policz jeszce raz te nierownosc pewnie bedza zle policzone miejsca zerowe

kamczatka: ok dzięki miałem źle policzone miejsca zerowe teraz jest ok i wychodzi x ∊<−6;−4)