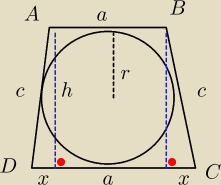
 Trapez równoramienny ABCD o podstawach AB i CD jest opisany na okręgu o promieniu r. Wykaż, że
4r2 = |AB|*|CD|
Matura, maj 2013.
Trochę koślawy ten trapez, ale wierzcie mi na słowo, że jest równoramienny i opisany na tamtym
okręgu
Trapez równoramienny ABCD o podstawach AB i CD jest opisany na okręgu o promieniu r. Wykaż, że
4r2 = |AB|*|CD|
Matura, maj 2013.
Trochę koślawy ten trapez, ale wierzcie mi na słowo, że jest równoramienny i opisany na tamtym
okręgu  Czy moje rozwiązanie to wystarczający dowód?
Teza: 4r2 = a*b
−−−−−−−−−−
Rozwiązanie:
Oznaczenia pomocnicze:
|AB| = a
|CD| = b
b = 2x + a
c − ramię trapezu
2r = h
4r2 = (2r)2 = h2
Z własności czworokąta, opisanego na okręgu:
a + b = 2c
a + a+2x = 2c
2a + 2x = 2c
c = a + x
Z tw. Pitagorasa:
h2 = c2 − x2
h2 = (a + x)2 − x2 = a2 + 2ax + x2 − x2 = a2 + 2ax
A więc mamy:
L = 4r2 = h2
P = a*b = a(2x + a) = a2 + 2ax
...co jest zgodne z tw. Pitagorasa, a więc co należało udowodnić?
Czy moje rozwiązanie to wystarczający dowód?
Teza: 4r2 = a*b
−−−−−−−−−−
Rozwiązanie:
Oznaczenia pomocnicze:
|AB| = a
|CD| = b
b = 2x + a
c − ramię trapezu
2r = h
4r2 = (2r)2 = h2
Z własności czworokąta, opisanego na okręgu:
a + b = 2c
a + a+2x = 2c
2a + 2x = 2c
c = a + x
Z tw. Pitagorasa:
h2 = c2 − x2
h2 = (a + x)2 − x2 = a2 + 2ax + x2 − x2 = a2 + 2ax
A więc mamy:
L = 4r2 = h2
P = a*b = a(2x + a) = a2 + 2ax
...co jest zgodne z tw. Pitagorasa, a więc co należało udowodnić?
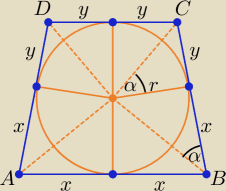 Szkic:
Szkic:
| y | r | ||
= | ⇒ r2 = x*y /*4 ⇒ 4r2 = 4xy = 2x * 2y = |AB| * |CD| | ||
| r | x |
 Błyskawiczne rozwiązanie
Błyskawiczne rozwiązanie  Ciekawe
Ciekawe 
 Jednak ponawiam moje pytanie, które nie było prośbą o inny sposób rozwiązania
Jednak ponawiam moje pytanie, które nie było prośbą o inny sposób rozwiązania  Czy to, co podałem, to jest pełnoprawny dowód?
Czy to, co podałem, to jest pełnoprawny dowód?
