czworoscian zadanie: Oblicz objetosc czworoscianu, ktorego wierzcholkami sa srodki scian czworoscianu ABCD , gdzie A=(1,2,0), B=(3,6,0), C=(4,1,1), D=(7,7,1). objetosc czworoscianu rozpietego na wektorach u, v, w jest rowna

	1
V=		|det(u, v, w)|.
	6

ale jak obliczyc w tym zadaniu te wierzcholki aby moc pozniej policzyc te wektory?

alfa i omega: u=AB=[2,4,0] v=AC=[3,−1,1] w=AD=[6,5,1]

zadanie: no tak to umiem zrobic ale najpierw trzeba obliczyc te wierzcholki tamtego czworoscianu bo jego objetosc musze obliczyc i jak bede miec juz te wierzcholki to wtedy oblicze wektory a pozniej pole tylko nie wiem wlasnie jak te wierzcholki obliczyc no bo pisze, ze wierzcholkami sa srodki scian czworoscianu ABCD ale jak je obliczyc? prosilbym o pomoc

zawodus: Środek trójkąta jak wyznaczyć?

zadanie: w sensie srodek ciezkosci trojkata?

zadanie:

	A+B+C
srodek ciazkosci trojkata o wierzcholkach A,B,C to
	3

no dobrze ale jak to wykorzystac? po co nam jest to potrzebne ? moge prosic o wytlumaczenie?

zadanie: ?

zadanie: ?

zawodus: "wierzchołkami są środki ścian czworościanu" − po to nam to potrzebne

zadanie:

	A+B+C
czyli		=E
	3

A+B+D
	=F
3

B+C+D
	=G
3

A+C+D
	=H
3

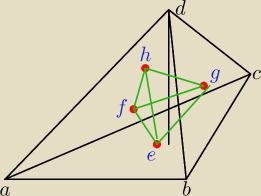
i to beda te punkty nowego czworoscianu? a gdzie te punkty beda na rysunku? dobrze je zaznaczylem?

zadanie: ?

zadanie: moge prosic o sprawdzenie?

zawodus: Wg mnie ok

zadanie: dziekuje

zadanie: czyli srodkiem sciany czworoscianu czyli srodkiem trojkata jest jego srodek ciezkosci tak?

zadanie: ?

AS: Moja propozycja (pod rozwagę − mogę się mylić) Rozpatrzmy podstawę ABC gdzie A = (1,2,0) , B = (3,6,0) C = (4,1,1) Środek tego trójkąta leży na przecięciu się środkowych tego trójkąta.Wspólny punkt dzieli każdy z nich w stosunku 2:1. Środek odcinka AB: D = (2,4,0) Zgodnie z podziałem odcinka w danym stosunku mamy

	x1 + k*x2
xk =
	1 + k

Dla odcinka CD:

	4 + 2*2		8
xc =		=
	3		3

	1 + 2*4
yc =		= 3
	3

	1 + 2*0		1
zc =		=
	3		3

Pierwszy środek wpisanej bryły: (8/3,3,1/3) Powtórzyć obliczenia dla pozostałych trzech wierzchołków i obliczyć objętość