Geometria analityczna - (nie)trywialne zadanie z okręgami V.Abel: Cześć, macie pomysł jak to wyznaczyć? Napisać równanie okręgu, który jest styczny do prostych o równaniach 2x+y−1=0 i 2x −y+2=0 oraz przechodzi przez pkt (0,0). Jak się za to w ogóle zabrać? Treść taka niby nic, bo znaleźć równanie, a tu takie cuda niewidy Pomożecie?

Saizou : odległość od prostych i od punktu (0:0) jest taka sama i wynosi r

Saizou : odległość od środka okręgu oczywiście

Mila: Jutro. Wieczorem. Trochę późno sie zjawiłeś.

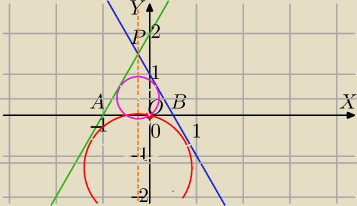
Utem: 2x+y−1=0 i 2x −y+2=0 k: y=−2x+1 m: y=2x+2 Punkt przecięcia prostych:

	−1		3
(		,		)
	4		2

Środek okręgu wpisanego w kąt leży na dwusiecznej kąta.

	−1
Dwusieczna kąta APB to prosta x=
	4

==================

	−1
S=(		,b) środek okręgu stycznego do ramion kata i przechodzącego przez O(0,0).
	4

|SO|=d(S,k)=d(S,m)

	−1
|SO|2=(		)2+b2
	4

	1   |2*(− )+b−1|   4		3   |b− |   2
d(S,k)=		=
	√22+12		√5

	−1		3   |b− |2   2
(		)2+b2=
	4		5

	−3−2√10		−3+2√10
b=		lub b=
	8		8

Pozostaje obliczyć r² i napisać równania, to pozostawiam Tobie. Masz odpowiedź? Sprawdź rachunki.