problem
Radek:
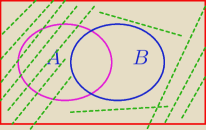
O zdarzeniach losowych A i B wiadomo, że P (A∪B)=0,9, P(A∩B)=0,3 i P(A∪B′)=0,5.Oblicz P(A′∪B)
.
P(A∪B')=0,5
P(A∪B')=jak to rozpisać
18 kwi 21:49
Mila:
P(AUB')=P(A)+P(B')−P(A∩B')
A∩B'=A\B
18 kwi 21:56
Radek: Dziękuję, może teraz wyjdzie
18 kwi 22:01
Mila:
Na pewno, tylko patrz uważnie na rysunek, najlepiej wpisuj tam znane wartości.
18 kwi 22:07
Radek:
Nie rozumiem tych primów
18 kwi 22:15
Mila:
(Radek) jest sam w swoim pokoju, wszystko poza tym pokojem to ( Radek)'.
18 kwi 22:30
Radek:
Ale ten zapis 21:56 mi się nie zgadza
P(A∪B')=1−P(B\A) ?
18 kwi 22:38
Mila:
To skorzystaj z Twojego.
18 kwi 22:58
Mila:
No i co, zrobiłeś?
18 kwi 23:10
Radek:
Tak, ale myślę nad tym Pani zapisem z 21:56 ?
18 kwi 23:13
Mila:
(1) P(AUB')=P(A)+P(B')−P(A∩B')
A∩B'=A\B
(2) P(A'UB)=P(A')+P(B)−P(A'∩B)
A'∩B=B\A
Dodajesz stronami (1) i (2) i wszystko pieknie wychodzi
18 kwi 23:17
Radek:
P(A'∩B)=P(A')+P(B)−P(B\A)
tego nie mogę sobie na diagramie zaznaczyć
18 kwi 23:19
Radek: ?
18 kwi 23:40
Mila:
skąd masz to równanie? 23:19
18 kwi 23:42
Radek:
23:17
18 kwi 23:45
Mila:
Inaczej pogrupowałam i mam tak:
P(AUB')+ P(A'UB)==P(A)+P(B')−P(A∩B')+P(A')+P(B)−P(A'∩B)
0,5+x=[P(A)+P(A')]+[P(B)+P(B')]−[P(A\B)+P(B\A)]⇔
0,5+x=1+1−[P(AUB)−P(A∩B)]
0,5+x=2−(0,9−0,3)
x=0,9
18 kwi 23:51
Radek:
Jest Pani jeszcze na forum ?
18 kwi 23:59
Mila:
Już znikam Radku, co chciałeś?
19 kwi 00:02
Radek:
Podziękować za pomoc i życzyć Wesołych Świąt !
19 kwi 00:06
Mila:
Dziękuję za życzenia, również ja Tobie życzę wesołych świąt i mokrego dyngusa
.
19 kwi 00:10
Radek:
Dziękuję.
19 kwi 00:12