456 julka: W trójkąt prostokątny o przyprostokątnych długości 8 i 12 wpisujemy prostokąty tak, że dwa boki prostokąta zawierają sie w przyprostokątnych trójkąta. Znajdź długości boków tego spośród prostokątów, który ma największe pole.

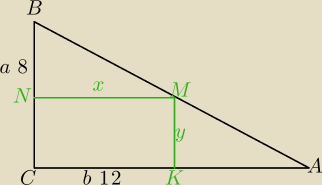
Mila: ΔBNM∼ΔBCA⇔

BN		a
	=		⇔
x		b

8−y		8
	=
x		12

8x=12*8−12y x=12−1,5y P=x*y P(y)=(12−1,5y)*y P(y)=12y−1,5y² funkcja ma największa wartość w wierzchołku paraboli

	−12
yw=
	2*(−1,5)

y_w=4 x=12−1,5*4=6 Szukane długości boków prostokąta; 6 i 4.

julka: ale jest, ze wpisujemy prostokatY, a ty masz jeden... chyba nie rozumiem: p

Draghan: Wpisujemy nieskończenie wiele prostokątów, które różnią się długością boków Ale "na raz" wpisany jest jeden A rysunek jest jedynie poglądowy, taka pomoc