prawd Technik: Mila, zawodus spojrzyjcie Wykaż, że jeśli A ,B są dowolnymi zdarzeniami przestrzeni Ω , to P (A ∪ B ) = P(A )+ P(B )− P(A ∩ B ) P(A)=P(A\B)+P(A∩B) P(B)=P(B\A)+P(A∩B) P(A∪B)=P(A)+P(B)−P(A∩B) P(A∪B)=P(A\B)+P(A∩B)+P(B\A)+P(A∩B)−P(A∩B) P(A∪B)=P(A\B)+P(B\A)+P(A∩B) C.N.W Tak to należy zapisać ?

zawodus: Nie możesz korzystać z tezy

Technik: Czyli jak mam to rozpisać ? P(A\B)+P(B\A)+P(A∩B)=P(A∪B) ?

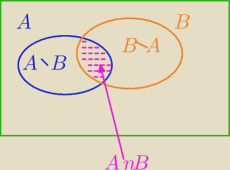
Mila: Z. A⊂Ω,B⊂Ω T. P (A ∪ B ) = P(A )+ P(B )− P(A ∩ B ) A\B, A∩B,B\A − trzy rozłączne zbiory, dołączam diagram⇔ P(AUB)=P(A\B)+P( A∩B)+P(B\A)⇔ P(AUB)=P(A)−P( A∩B)+P( A∩B)+P(B)−P(A∩B)⇔ P(AUB)=P(A)+P(B)−P(A∩B) cnw

Technik: To co ja robię źle ?

Mila: Przeczytaj co Ci napisałam, to zobaczysz różnicę .

zawodus: W twoim pierwszym poście korzystasz z tezy. Tak nie wolno, bo wtedy zawsze otrzymasz to co chcesz niezależnie od tego jaką głupotę weźmiemy za tezę

Technik: P(A) i P(B) takim zdarzeniami losowymi zawartymi w Ω , że P (A ∖ B) = P (B ∖A ) = 17 i P(A ′ ∪ B ′) = 1 . Oblicz P (A ′ ∩ B ′)

	1
P(A\B)=P(B\A)=
	7

P(A'∪B')=1 1−P(A∩B)=1 P(A∩B)=0

	1
P(A)=P(A\B)+P(A∩B)=
	7

	1
P(A)=
	7

	1
P(B)=
	7

P(A'∩B')=1−P(A∪B) P(A∪B)=P(A)+P(B)−P(A∩B)

	2
P(A∪B)=
	7

	5
P(A'∩B')=		?
	7

Technik: Ok, już widzę różnicę

Mila: 16:45 dobrze. II Mogłeś skorzystać z wzoru: P(A'UB')=P(A')+P(B')−P(A'∩B')

	1		1
1=1−		+1−		−P(A'∩B')
	7		7

5
	=P(A'∩B')
7