Oblicz długość promienia okręgu opisanego na trójkącie BCD
Łukasz:
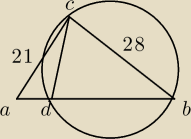
W trójkącie prostokątnym ABC przyprostokątne mają długości |BC|=28, |CA|=21. Na boku AB wybrano
punkt D tak, że poletrójkąta ADC jest równe 126. Oblicz długość promienia okręgu opisanego na
trójkącie BCD.
mam jedno pytanie, czy ten rysunek jest poprawny

18 kwi 16:09
razor: tak
18 kwi 16:17
Łukasz: Mam pewien pomysł na to zadanie ale nie wiem czy dobrze myślę..
mianowicie:
Zajmę się najpierw trójkątem ADC, wiemy, że jego pole wynosi 126.
h=12
skorzystam z tw.Pitagorasa i obliczę dł. odcinka CD
y
2=
√585=3
√65
| | 28 | |
Mogę teraz obliczyć długość kąta DBC, cosα= |
| |
| | 35 | |
Teraz mogę obliczyć długość odcinka DB z twierdzenia cosinusow:
| | 28 | |
585=784+1225−70x+x2−(1960−56x)* |
| |
| | 35 | |
| | 4 | |
585=2009−70x+x2−1568+44 |
| x |
| | 5 | |
5x
2−126x−720=0
Δ
x=15876+14400
√Δ=174
x
1<0
x
2=30
|DB|=30
Odpowiedź: długość promienia okręgu opisanego na tym trójkącie wynosi 15.
Wynik niby wyszedł ładny ale ciekawe czy rzeczywiście jest dobrze, proszę o sprawdzenie
18 kwi 17:59
Piotr 10: wynik zły R=10√2
18 kwi 18:02
Łukasz: teraz pytanie, czy cały ten sposób jest do bani czy gdzieś błąd w obliczeniach?
18 kwi 18:23
Łukasz: hmm? ewentualnie poproszę o jakąś wskazówkę to postaram się zrobić to innym sposobem.
18 kwi 18:42
Mila:
Łukasz, źle to masz.
Najpierw zastanów się, co możesz obliczyć mając te dane.
Jeśli się zjawisz, to dalej dam wskazówki.
18 kwi 21:38
matura: Milu, już wszystko wiem.
Obliczam wysokość, korzystam z Tw. Talesa |AD|=15 |BD|=20
wyliczam sinβ cosβ
teraz z tw. cos odcinek |CD| po czym mogę skorzystać z twierdzenia sinusow:
i z tego wychodzi 10
√2.
Bardzo przyjemne zadanie, nie pomyślałem o tym Talesie tutaj, dziękuje mimo wszystko

19 kwi 13:16
pigor: ... Pitagoras pogniewałby się kolego, bo nie widać tu nigdzie Talesa.
19 kwi 17:01
Utem:

19 kwi 21:55
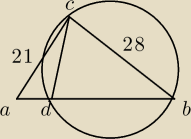 W trójkącie prostokątnym ABC przyprostokątne mają długości |BC|=28, |CA|=21. Na boku AB wybrano
punkt D tak, że poletrójkąta ADC jest równe 126. Oblicz długość promienia okręgu opisanego na
trójkącie BCD.
mam jedno pytanie, czy ten rysunek jest poprawny
W trójkącie prostokątnym ABC przyprostokątne mają długości |BC|=28, |CA|=21. Na boku AB wybrano
punkt D tak, że poletrójkąta ADC jest równe 126. Oblicz długość promienia okręgu opisanego na
trójkącie BCD.
mam jedno pytanie, czy ten rysunek jest poprawny

