123
joolka:
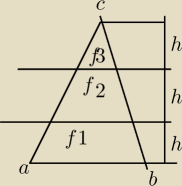
trojkat ABC podzielono 2 prostymi rownoleglymi do podstawy trojkata na trzy figury F1, F2, F3 o
polach odpowiednio P1, P2, P3. wyznacz stosunek P2/P3
18 kwi 15:36
zawodus: Podobieństwo

18 kwi 15:38
J: Rysunek myli... figury nie mogą mieć tej samej wysokości h ..
18 kwi 15:42
joolka: tak jest w ksiazce

18 kwi 15:57
joolka: wiec?

18 kwi 17:57
Tadeusz:
P2+P3=4P3 ⇒ P2=3P3 P2/P3=
18 kwi 18:06
joolka: skad to P2+P3=4P3 ?
18 kwi 18:15
Tadeusz:
... ze skali podobieństwa
18 kwi 18:17
Mila:
Stosunek pól figur podobnych jest równy kwadratowi skali podobieństwa.
P=P
ΔABC
| | 1h | | 1 | |
F3∼ΔABC w skali k= |
| = |
| ⇔ |
| | 3h | | 3 | |
| | 2h | | 2 | |
Trójkąt , ktory jest sumą F2 i F3 jest podobny do ΔABC w skali k1= |
| = |
| ⇔ |
| | 3h | | 3 | |
Tak samo masz u
Tadeusza
18 kwi 19:53
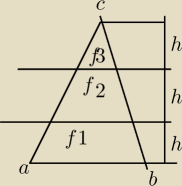 trojkat ABC podzielono 2 prostymi rownoleglymi do podstawy trojkata na trzy figury F1, F2, F3 o
polach odpowiednio P1, P2, P3. wyznacz stosunek P2/P3
trojkat ABC podzielono 2 prostymi rownoleglymi do podstawy trojkata na trzy figury F1, F2, F3 o
polach odpowiednio P1, P2, P3. wyznacz stosunek P2/P3


