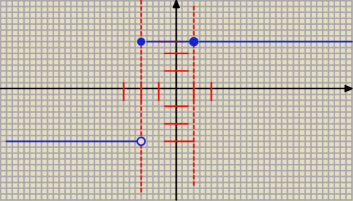
Funkcje Kamix: Cześć. Mam problem z narysowaniem podanej funkcji: f(x)=|x+2|+|1−x| Rozpatruję ją na trzy przypadki: 1 przypadek: f(x)∊(−∞;−2) f(x)=−x−2−1+x f(x)=−3 2 przypadek: f(x)∊<−2;1) f(x)=x+2+1−x f(x)=3 3 przypadek: f(x)∊<1;+∞) f(x)=x+2+1−x f(x)=3 Zabieram się za rysowanie: Według mnie wykres powinien wyglądać tak jak to ja narysowałem, jednak wolphramalpha pokazuje inaczej, a on się raczej nie myli... Gdzie popełniam błąd?

J: 2 przypadek .. źle

J: Nie drugi ... trzeci źle.

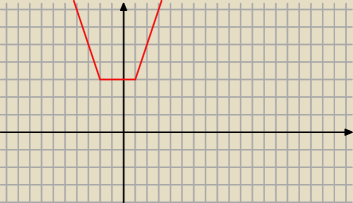
5-latek: Taki ma byc wykres tej funkcji

J: Racja ... pierwszy przypadek też był źle

Kamix: Wykres wiem, że tak będzie wyglądał, bo pokazał mi to wolphram. A możesz 5−latek rozpisać to w ten sposób co ja, bym mógł zobaczyć co robiłem źle...

Kamix: ponawiam...

5-latek: Mozesz to |1−x| zapisac jak |x−1| A robiles zle juz tu dla 1 przedzialu np (−oo −2) y= |x+2|+|1−x| to |x+2|= −(x+2)=−x−2 natomiast |1−x| to wezmy np liczbe x=−5 bo ona nalezy do tego przedzalu to dostaniemy tak |1−(−5)|= |1+5|=|6|=6 czyli dla tego przedzialu |1−x|=1−x wiec dla tego przdzialu x nalezy (−oo −2) y= |x+2|+|1−x| to y= −x−2+1−x to y= −2x−1

Kamix: Ahhh tak, okey dziękuję bardzo, postaram się zastosować do Twoich wskazówek, mam nadzieję, że wyjdzie dobrze ; DD

Marcin: 1 przypadek: −x−2+1−x=f(x) −2x−1=f(x) Podstaw sobie za x=−10 i zobaczysz, że źle zmieniasz znaki. Jeden moduł będzie dodatni, a drugi ujemny.

Marcin: ehh. Zawsze spóźniony Witam

Kamix: Liczą się chęci Marcinie ; DD Oczywiście doceniam ; )

5-latek: Ten zapis |1−x|=|x−1| wynika z takiej wlasnosci wartosci bezwzglednej |a−b|=|b−a|

5-latek: Czesc Marcin

Marcin: Jak masz wątpliwości, to zawsze podstawiaj liczbę z każdego przedziałów i sprawdzaj czy moduł jest dodatni czy ujemny.

Kamix: No i udało mi się dzięki Wam poprawnie rozwiązać zadanko ; D Dziękuję!

Kamix: Zazwyczaj Marcin nie miałem problemów z rozwiązywaniem równań i nierówności z wartością bezwzględną, ale tutaj zmylił mnie ten drugi moduł ; D Oczywiście wszystko rozumiem, dzięki 5−latek

5-latek: Marcin raczej bym nie uzywal stwierdzenia modul (choc sam tego uzywalem Przeczytalem o tym niedawno ze okreslenie modul odnosi sie do mnozenia i dodawania (ze modulem dodawania jest liczba 0 a modulem mnozenia jest 1 ) Ze powinno sie uzywac okreslenia wartosc bezwzgledna . Ale juz sam nie wiem moze ktos przeczyta jeszcze ten post i sie wypowie .

Marcin: To takie przyzwyczajenie Postaram się z tym walczyć