dowód
bezendu:
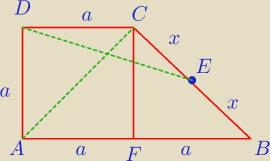
Chyba tego nigdy nie zrozumiem
Wysokość CF trapezu prostokątnego ABCD dzieli trapez na kwadrat i trójkąt prostokątny
równoramienny Niech E będzie środkiem ramienia BC Uzasadnij, że przekątna AC dzieli odcinek DE
na pół
DC=a
√2
17 kwi 23:11
17 kwi 23:23
bezendu:
Jestem idiotą z planimetrii i nic nie rozumiem z niej.
17 kwi 23:27
Domel: Spoko − no panic − co wiesz o przekątnych równoległoboków
17 kwi 23:31
bezendu:
Dzielą się na równe części .
17 kwi 23:33
Domel: 
17 kwi 23:37
bezendu:
I to koniec zadania ?
17 kwi 23:39
Marcin: Musisz jeszcze jakoś formalnie udowodnić, że to jest równoległobok
Rysunek w dowodach nie
działa.
17 kwi 23:40
Domel: No mój rysunek musi mieć opis i dodatkową literkę np. G na złączu fioletowych linii a H na
przecięciu zielonych przekątnych. A potem piszesz:
|EG| = |DC| ∧ |DG| = |CE| => |DH| = |HE| ∧ |GH| = |HC| z tw. o przekątnych
równoległoboku.
i już
− przynajmniej wg mnie
17 kwi 23:46
bezendu:
Dzięki, ale jak na to wpadłeś ? Coś czuje, że na maturze 10% pójdzie się...
17 kwi 23:48
Bogdan:
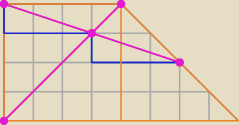
a teraz widać?
17 kwi 23:54
bezendu:
Szczerze ? To nie
17 kwi 23:56
Domel: Zauważ, że ukośna fioletowa (w moim rysunku) jest połową przekątnej kwadratu − więc tę drugą
przekątną |AC| dzieli na pół a odcinek |CB| w trójkącie prostokątnym równoramiennym odpowiada
długością przekątnej kwadratu − a punkt E leży w połowie |CB|
18 kwi 00:10
bezendu:
Dzięki Domel.
18 kwi 00:12
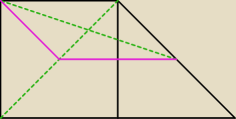Czy to coś wyjaśnia