Środkowe trójkąta/ stosunki pól Ania: W trójkącie ABC poprowadzono trzy środkowe, które podzieliły trójkąt na sześć małych trójkątów. Jaką część pola trójkąta ABC stanowi pole każdego z tych trójkątów.

Domel: Gdzie się przecinają środkowe i co to znaczy

BoosterXS: Środkowe trójkąta przecinają się w punkcie S, który nazywamy środkiem ciężkości trójkąta. Punkt S dzieli każdą ze środkowych na dwie części, z których odcinek łączący wierzchołek z punktem S jest dwa razy dłuższy od pozostałej części tej środkowej Troche teori, mam nadzieje, że cos pomoże

Ania: chyba jednak nic, teorie znam dość dobrze, gdyby był równoboczny sprawa rozwiązałaby się dość szybko no ale nie jest więc środkowe nie są sobie równe i dlatego nie wiem na czym się oprzeć

Domel: No cóż − skoro środkowe przecinają się w środku ciężkości trójkąta to trójkąt musi być „wyważony” względem tego punktu czyli małe trójkąciki muszą się równoważyć więc są takie same.

	1
A ponieważ jest ich 6 to pole każdego z nich wynosi		dużego trójkąta
	6

toja: To nie jest dowód matematyczny

5-latek: to jest zadanie z olimpiady . Piotr10 pokazywal link . Wiec Aniu szukaj sama rozwiazan

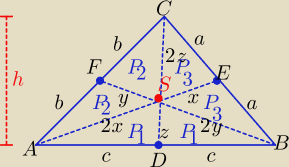
Eta: Każda środkowa dzieli trójkąt na dwa trójkąty o równych polach P(ADC)=2P₂+P₁=P(DBC)=2P₃+P₁ ⇒ P₂=P₃ ⇒P₁=P₂=P₃ P(AEC)=2P₂+P₃=P(ABE)=2P₁+P₃ ⇒ P₁=P₂ zatem: ...........