Ostrosłup czworokątny. anonim: Dany jest ostrosłup prawidłowy czworokątny. Wysokość jest dwa razy dłuższa od krawędzi podstawy wyznacz cosinus kąta między dwiema sąsiednimi ścianami bocznymi tego ostrosłupa.

	3
Ściana boczna wyszła		a, gdzie a to krawędź podstawy. Pomoże ktoś?
	2

PW:

	3
Ściana boczna		a? Co to znaczy?
	2

Piotr: tez sie nad tym zastanawiam

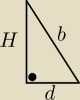
anonim: H = 2a

	a√2
d − połowa przekątnej, czyli
	b

b² = H² + d ²

	a√2		a2		9
b2 = 4a2 +		= 4a2 +		=		a2
	2		2		4

	3
b =		a
	2

anonim: Ups, krawędź boczna* moja wina

PW: Zasadnicze moje "wybrzydzanie" w takich wypadkach polega na pytaniu: − A po co to liczyłeś? Może w ogóle nie jest potrzebne do rozwiązania? Zadania powinno się rozwiązywać metodą "byka za rogi". Pytają o kosinus jakiegoś kąta − no to staram się zobaczyć ten kąt i zastanawiam się jak policzyć ten kosinus. Stawiamy sobie pierwsze pytanie − co to jest kąt między dwiema płaszczyznami i gdzie go w tym zadaniu inteligentnie narysować?

Piotr: juz to masz źle.

	a2		8		a2		9
b2 = 4a2 +		=		a2 +		=		a2
	2		2		2		2

	3√2
b =
	2

Piotr: 'a' na koncu sie zgubilo

PW: Nie sprawdzałem, bo na razie nie widzę celowości liczenia tego. Równie dobrze można policzyć objętość ostrosłupa − tylko po co?

Piotr: a ja tam nie wiem. mam wrazenie, ze anonim policzyl pierwsze co przyszlo mu na mysl. i jeszcze źle to zrobil.

PW: No to czekamy na rysunek w wykonaniu anonima − gdzie jest ten kąt?

anonim: no właśnie tu jest problem, bo nie wiem który to kąt. Piotr − mój błąd przepraszam po raz drugi

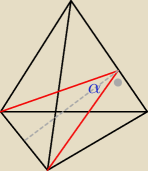
Marcin: o tu

anonim: Jest to ostrosłup czworokątny, nie trójkątny.

PW: Nie umiem tu rysować, ale podpowiem. Kąt między dwiema płaszczyznami jest zdefiniowany jako kąt płaski na płaszczyźnie prostopadłej do wspólnej krawędzi tych płaszczyzn wyznaczony przez wspólne krawędzie każdej z tych płaszczyzn i płaszczyzny prostopadłej. Piękne. Mówiąc praktycznie − trzeba poprowadzić płaszczyznę prostopadłą do krawędzi tych dwóch płaszczyzn, zostanie na niej wyznaczony kąt zwany kątem między płaszczyznami. Poprowadzić tę płaszczyznę prostopadłą można gdziekolwiek, np. w połowie krawędzi bocznej albo trochę wyżej. Trzeba to zrobić inteligentnie − tak, żeby związać przekrój ze znanymi odcinkami (lub takimi, które łatwo obliczyć).

Marcin: No ok, pomyliłem się. Potraktuj mój rysunek jako podpowiedź

PW: No właśnie, Marcin zrobił to dobrze, chociaż nie w takim ostrosłupie.

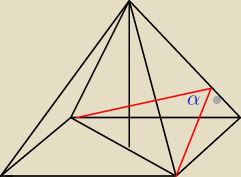
Marcin: Ok. Skończę co zacząłem

anonim: Mhm, to postaram się coś zrobić

PW: No, a ten kącik prosty bierze się z twierdzenia o trzech prostopadłych i definicji płaszczyzny prostopadłej do prostej. Widać więc, że dla wyznaczenia cosα z twierdzenia kosinusów trzeba obliczyć długości czerwonych odcinków − to jest celowe. Nie wykluczam, że dla osiągnięcia tego może być potrzebna długość krawędzi bocznej, ale to się dopiero okaże.

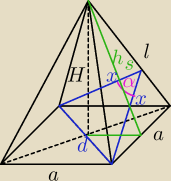
dero2005: H = 2a

	a
hs = √(a2)2 + (2a)2 =		√17
	2

	3a
l = √(a2)2 + hs2 =		√2
	2

a*h_s = x*l

	a*hs		a
x =		=		√34
	l		6

d = a√2 d² = 2x² − 2x²cosα 2a² = 2x² − 2x²cosα

	a2
cosα = 1 −		= −117
	x2

sprawdź wyniki