matma kyrtap: Pomoże mi ktoś z arkuszem bo te zadania jak dla mnie są trudne

bezendu: Jasnowidz proszony do tematu !

kyrtap: Mogę podawać zadania? Włączam zegar, zagrajmy

Godzio:

Marcin: Ok, jestem. Pierwsze zadanie nie jest trudne

bezendu: Dawaj Sacha !

daras: mam szkalną kulę tylko trochę zakurzona

kyrtap:

	1		1		1		1
Rozwiąż nierówność		+		+		+		+
	x(x+1)		(x+1)(x+2)		(x+2)(x+3)		(x+3)(x+4)

	1
		< 0
	(x+4)(x+5)

Piotr 10:

	1		1		1
zauwaz, że		=		−		itd. poskraca Ci się po drodze
	x(x+1)		x		x+1

Piotr: ale to juz bylo

kyrtap: nie wiedziałem

kyrtap: Pewnie ten arkusz rozwiązywałeś Piotrze?

Marcin: Co to za maturka? też chce!

kyrtap: szczerze powiedziawszy bym tego nie zauważył na maturze

Piotr 10: Chyba tak, to z Pazdro ?

kyrtap: http://www.tomaszgrebski.pl/arkusze/PAZDRO/2009%20PR.pdf

kyrtap: tak

bezendu: A teraz czekamy na tę trudne zadania...

Marcin: Dzięki Chyba przeoczyłem ten arkusz

kyrtap: następne włączam zegar

kyrtap: W prostokątnym układzie współrzędnych zaznacz zbiór tych wszystkich punktów płaszczyzny o

	ax+2
współrzędnych (a,b) , dla których funkcja f (x) =		jest funkcją homograficzną,
	x+b

malejącą w każdym z przedziałów: (− ∞ ,2),(2,+ ∞ ) .

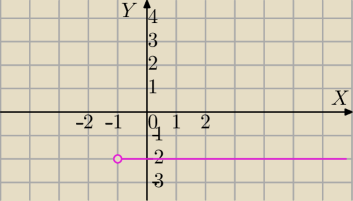
Mila: x=2 jest punktem nieciągłości− asymptota pionowa

	ax+2
f(x)=		⇔b=−2
	x−2

	ax−2a +2a+2
f(x)=
	x−2

	a*(x−2)+2a+2
f(x)=
	x−2

	2a+2
f(x)=a+
	x−2

f(x) malejąca w przedziałach⇔2a+2>0 ⇔a>−1 P(a,−2) i a>−1

kyrtap: 3 zadania z tego arkusza mi uciekły dziękuje za pomoc

kyrtap: Może dacie jakieś zadanko dowodowe do zrobienia ?

jerey: dowód ze stereometrii Na płaskiej powierzchni położono trzy kule K1,K2,K3 , każda o promieniu 2 tak, że kule K1 i K2 są styczne w punkcie P3 , kule K2 i K3 są styczne w punkcie P1 , a kule K3 i K1 są styczne w punkcie P2 . Następnie położono na tych kulach kulę K4 o promieniu 3, która jest styczna do kul K1 ,K2 ,K3 odpowiednio w punktach S1,S2,S3 . Uzasadnij, że odcinki P1P2 i S1S2 są równoległe.