Funkcja kwadratowa problem ze zbiorem wartosci marian: Witam mam problem z wyznaczeniem zbioru wartości funkcji g. Dana jest funkcja kwadratowa f(x)=(m+2)x² + (3m−2)x + 1. Wyznacz w zależności od parametru m

	1		1
wzór funkcji g(x) =		+		, gdzie x1 i x2 sa roznymi miejscami zerowymi funkcji
	x1		x2

f. Podaj dziedzinę z zbiór wartości funkcji g. Wychodzi mi g(m)= −3m + 2

	2
oraz dziedzina D = (−∞, −		) u ( 2, +∞) \ { − 2 }
	9

co sie zgadza w odpowiedziach ale nie moge zrozumieć czemu zbiór wartości jest

	8
Zw = (−∞, 4) u (		, +∞ ) \ {8}
	3

wmboczek: 2/9 z D odpowiada końcowi 8/3 ze Zw

Mila:

	−2
D=(−∞,−2)U(−2,		)U(2,∞)
	9

f(−2)=−3*(−2)+2=8 argument (−2) nie należy do dziedziny, to odrzucamy tę wartość

	2		2
f(−		)=2		tez odrzucamy tę wartość
	9		3

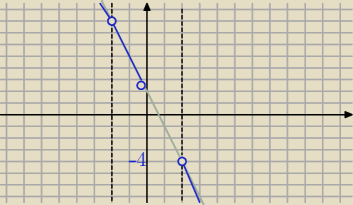
f(2)=−3*2+2=−4 odrzucamy tę wartość Zbiór wartości (od dołu osi OY)

	8
Zw=(−∞,−4)U(		,8)U(8,∞)
	3