okrąg
Radek:
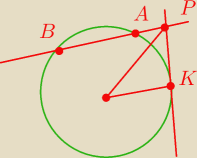
ZZ punktu P, którego odległość od środka O okręgu jest równa 5cm, poprowadzono styczną do
okręgu w punkcie K oraz sieczną przecinającą okrąg w punktach A i B. Wiedząc, że promień
okręgu ma długość 3cm i |BP|

AP|=3:2, oblicz długość odcinka AB.
PK=4
(3x)
2+(2x)
2=16
13x
2=16
x=U{4
√13}[13}
ale źle mam ?
16 kwi 23:20
Radek: ?
16 kwi 23:28
zawodus: Twierdzenie o stycznej i siecznej.
16 kwi 23:28
Radek:
z tego właśnie skorzystałem
BP2*AP2=PK2
16 kwi 23:29
Radek: źle
3x*2x=4
2
6x
2=16
16 kwi 23:30
zawodus: ok

16 kwi 23:36
Radek:
Zawodus będziesz jeszcze ?
16 kwi 23:40
Mila:
No tak, ale dodałeś zamiast pomnożyć, niema tam tylu kwadratów we wzorze.
Masz z tw.
|PK|2=|AP|*|BP|
2x*3x=42
6x2=16
teraz dokończ.
16 kwi 23:40
zawodus: Mogę jeszcze trochę być

16 kwi 23:41
Radek:
Teraz już dokończyłem. Ale mam podobne zadanie i nie wiem jak zrobić:
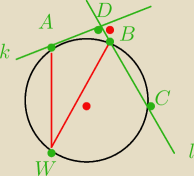
Prosta k jest styczna do okręgu w punkcie A. Prosta l, prostopadła do prostej k, przecina okrąg
w punktach B i C, zaś prostą k w punkcie D, tak że |BC| = 4,8|AD|. Oblicz tangens kąta ostrego
AWB wpisanego w dany okrąg
16 kwi 23:45
zawodus: W czym problem?
16 kwi 23:54
Radek:
Nie mogę z twierdzenia stycznej i siecznej bo mam 2 niewiadome ?
16 kwi 23:55
zawodus: Kąt AWB i ACB to to samo

17 kwi 00:07
zawodus: Wykorzystujemy twierdzenie

17 kwi 00:08
Radek:
Ale ja potrzebuje odcinka a nie kąta ?
17 kwi 00:13
zawodus: Ale TG policzysz z trójkąta prostokątnego. Masz odpowiedź?
17 kwi 00:15
Radek:
Nie do tego nie mam.
17 kwi 00:18
zawodus: Jutro ok?
17 kwi 00:19
zawodus: Bo spać mi się chce. Spróbuj policzyć tg kąta ACB. Masz trójkąty prostokątne i twierdzenie o
stycznej i siecznej.
17 kwi 00:21
Radek: dobra, ja i tak porobię jeszcze arkusze
17 kwi 00:21
Radek: ?
17 kwi 17:41
Mila:
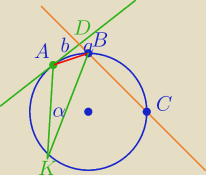
|AD|=a
|DB|=b
|BC|=4,8*b
Kąt między styczną a cięciwą AB jest równy kątowi wpisanemu opartemu na te cięciwie.⇔
∡DAB=α
Z tw. ostycznej i siecznej:
b
2=a*(a+4,8b) /:b
2
tgα*(tgα+4,8)=1 i tgα>0
rozwiąż.
17 kwi 18:16
Radek:
Trzeba rozwiązać równanie ?
17 kwi 18:17
Mila:
No tak, podstaw tgα=t, t>0
Masz przecież obliczyć tgα.
17 kwi 18:19
Radek:
Ok, nie znoszę trygonometrii.
17 kwi 18:19
17 kwi 18:22
Mila:
Zgadza się z moimi obliczeniami, a masz w podręczniku odpowiedź?
17 kwi 18:23
Radek:
Nie mam, to zadanie z arkusza.
17 kwi 18:26
zawodus: ODpowiedź prawidłowa.
17 kwi 20:16
Mila:
Dziękuję,
Zawodus 
17 kwi 20:25
Radek:
A mogę prosić jeszcze raz o wytłumaczenie tego zbioru wartości co wczoraj wstawiłem ?
17 kwi 20:25
 ZZ punktu P, którego odległość od środka O okręgu jest równa 5cm, poprowadzono styczną do
okręgu w punkcie K oraz sieczną przecinającą okrąg w punktach A i B. Wiedząc, że promień
okręgu ma długość 3cm i |BP|
ZZ punktu P, którego odległość od środka O okręgu jest równa 5cm, poprowadzono styczną do
okręgu w punkcie K oraz sieczną przecinającą okrąg w punktach A i B. Wiedząc, że promień
okręgu ma długość 3cm i |BP| AP|=3:2, oblicz długość odcinka AB.
PK=4
(3x)2+(2x)2=16
13x2=16
x=U{4√13}[13}
ale źle mam ?
AP|=3:2, oblicz długość odcinka AB.
PK=4
(3x)2+(2x)2=16
13x2=16
x=U{4√13}[13}
ale źle mam ?


 Teraz już dokończyłem. Ale mam podobne zadanie i nie wiem jak zrobić:
Prosta k jest styczna do okręgu w punkcie A. Prosta l, prostopadła do prostej k, przecina okrąg
w punktach B i C, zaś prostą k w punkcie D, tak że |BC| = 4,8|AD|. Oblicz tangens kąta ostrego
AWB wpisanego w dany okrąg
Teraz już dokończyłem. Ale mam podobne zadanie i nie wiem jak zrobić:
Prosta k jest styczna do okręgu w punkcie A. Prosta l, prostopadła do prostej k, przecina okrąg
w punktach B i C, zaś prostą k w punkcie D, tak że |BC| = 4,8|AD|. Oblicz tangens kąta ostrego
AWB wpisanego w dany okrąg


 |AD|=a
|DB|=b
|BC|=4,8*b
Kąt między styczną a cięciwą AB jest równy kątowi wpisanemu opartemu na te cięciwie.⇔
∡DAB=α
|AD|=a
|DB|=b
|BC|=4,8*b
Kąt między styczną a cięciwą AB jest równy kątowi wpisanemu opartemu na te cięciwie.⇔
∡DAB=α
