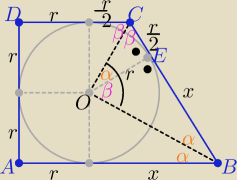
 2α+2β=180o , α+β=90o
Trójkąt BOC jest prostokątny
Z podobieństwa trójkątów BOE i EOC
2α+2β=180o , α+β=90o
Trójkąt BOC jest prostokątny
Z podobieństwa trójkątów BOE i EOC
| r |
| r | |||||||||
= | ⇒ r2=x* | ⇒ x=2r | |||||||||
| x | r | 2 |
| 3 | ||
|AB|=3r , |DC|= | r , h=2r | |
| 2 |
 Skąd wiemy że te trójkąty są podobne? Że kąt EOB=kątowi
OCE? I skąd wiemy że kąt EOC=kątowi EBO. No i jak wyprowadziłeś że OB jest dwusieczną?
Skąd wiemy że te trójkąty są podobne? Że kąt EOB=kątowi
OCE? I skąd wiemy że kąt EOC=kątowi EBO. No i jak wyprowadziłeś że OB jest dwusieczną?
 1/ gdzie znajduje się środek okręgu wpisanego w trapez?
2/ jakie znasz cechy podobieństwa trójkątów?
3/ w trójkącie prostokątnym suma kątów α+β= 90o, to.......
Powtórz koniecznie teorię ..........
1/ gdzie znajduje się środek okręgu wpisanego w trapez?
2/ jakie znasz cechy podobieństwa trójkątów?
3/ w trójkącie prostokątnym suma kątów α+β= 90o, to.......
Powtórz koniecznie teorię ..........
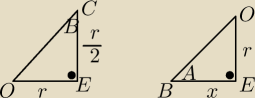 Z dwusiecznymi zrozumiałam, ale na tych dwóch trójkątach jak wyznaczyć podobieństwo? Cechy
podobieństaw to BBB, KK, BKB, a tu są tylko wiadome : bok r, i kąt prosty.
Z dwusiecznymi zrozumiałam, ale na tych dwóch trójkątach jak wyznaczyć podobieństwo? Cechy
podobieństaw to BBB, KK, BKB, a tu są tylko wiadome : bok r, i kąt prosty.
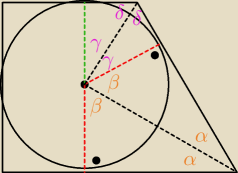 podobieństwo kąt, kąt, kąt
kluczem jest zauważenie, że α+β = 90 a to wynika z ... (rysunek)
zauważ, że: 2β+2γ = 180 ('półokrąg') −> β+γ = 90
ale z trójkąta widzisz, że α+β = 90
stąd γ =α (a co za tym idzie) β=δ
podobieństwo kąt, kąt, kąt
kluczem jest zauważenie, że α+β = 90 a to wynika z ... (rysunek)
zauważ, że: 2β+2γ = 180 ('półokrąg') −> β+γ = 90
ale z trójkąta widzisz, że α+β = 90
stąd γ =α (a co za tym idzie) β=δ